Численные методы интегрирования: Методические указания к выполнению лабораторной работы № 5, страница 5

Её остаточный член имеет выражение:

                                                                             

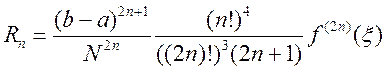
 Определим теперь порядок аппроксимации метода. Уменьшим разбиение сетки в 2 раза, то есть увеличим N в 2 раза. Получим уменьшение погрешности в  раза. То есть порядок аппроксимации равен 2n.

Правило Рунге практической оценки погрешности.

            Пусть  - неизвестное точное значение некоторой величины,  - известное ее приближенное значение (приближенное решение), зависящее от положительного параметра , который может принимать сколь угодно малые значения. Предположим, что установлена связь(соотношение)

                                                                                 

где  - неизвестная, не зависящая от  постоянная,  - известные числа.

(Это соотношение можно получить для любого метода интегрирования, учитывая производные более высоких порядков, в этом случае- порядок аппроксимации метода).

Тогда также справедливо

                                                                      

Вычитая равенства и , находим

. Отсюда

                                                                    

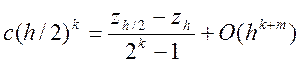
И, следовательно, согласно с точностью до  имеем

                                                                                      

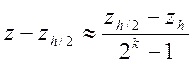
где  - известные величины.

Вычисление приближенной оценки погрешности по формуле при выполнении условия называется правилом Рунге.

Уточнение приближенного решения по Ричардсону.

Вычитая из умноженного на  равенства равенство , получаем

. Откуда

                                                                                        

где

.                                                                                       

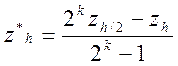Число  называется уточненным (экстраполированным) по Ричардсону приближенным значением величины .

Согласно разность  имеет в точности -й порядок относительно . В то же время, если в , то разность  имеет в точности -й порядок относительно .

Это говорит о том, что при применении уточнения по Ричардсону для некоторого метода интегрирования, повышает порядок точности этого метода как минимум на 1 (в общем случае на ). Объясняется это тем, что при уточнении по Ричардсону погрешность (а это разность ) имеет порядок больший чем , значит, эта погрешность будет равна нулю для многочленов степени меньшей .

Таким образом, зная вычисленные приближенные решения  и , и при наличии условия , где , можно

1.  Приближенно оценить погрешность  по правилу Рунге

2.  Вычислить приближенное решение , имеющее погрешность более высокого порядка малости относительно , чем .

Особенности вычисления интегралов с помощью компьютера

            При вычислении интеграла с помощью методов численного интегрирования на компьютере мы не можем не учитывать и погрешности хранения и преобразования данных в компьютере. На некоторых величинах в компьютере происходят ошибки округления или переполнения, этим вызвана необходимость введения следующего понятия.

Зона сходимости

Некоторое множество сеток, на которых приближенное значение интеграла сходится к точному, то есть практический порядок аппроксимации метода не отличается от теоретического более чем на 10%.

            Только в зоне сходимости мы можем воспользоваться оценкой погрешности по Рунге и уточненного решения по Ричардсону, т.к. на других сетках наш метод работает с заведомо большими погрешностями со стороны вычислительной машины.

Для приближенного значения можно записать

                                                                                 

где c не зависит от h, k – порядок аппроксимации метода, m – некоторая постоянная.

Согласно правилу Рунге