Численные методы интегрирования: Методические указания к выполнению лабораторной работы № 5

Методические указания

к выполнению лабораторной работы  №5

«Численные методы интегрирования»

Цель работы: Изучение методов численного интегрирования, оценки погрешности по правилу Рунге, оценки порядка аппроксимации, уточнения значений по Ричардсону.

Задание: Разработать программы, реализующие численное интегрирование заданной пользователем функции различными методами (по вариантам). Оценить порядок аппроксимации метода по нескольким интегрируемым функциям и сравнить его с теоретическим. Оценить погрешность по правилу Рунге. Уточнить значения интеграла по Ричардсону и сравнить с точным значением. Изучить влияние сгущения сетки в местах осцилляции функции. При разработке тестов использовать функции, интеграл от которых вычисляется аналитически.

Требования к реализации: Функцию задавать в виде подпрограммы, все остальные входные данные (сетку, отрезок и т.д.) вводить из файла. При реализации учесть возможность задания неравномерного шага интегрирования.

            Всего в вариантах заданий рассмотрено шесть методов численного интегрирования:

·  Метод прямоугольников

·  Метод трапеций

·  Метод Симпсона

·  Метод Гаусса-2

·  Метод Гаусса-3

·  Метод Гаусса-4

Содержание

Основные определения. 3

Каноническая формула прямоугольников. 4

Усложненная квадратурная формула прямоугольников. 4

Каноническая квадратурная формула трапеций. 5

Усложненная квадратурная формула трапеций. 6

Каноническая формула Симпсона. 6

Усложненная квадратурная формула Симпсона. 7

Многочлены Лежандра. 7

Интерполяционный многочлен Лагранжа. 8

Каноническая квадратурная формула Гаусса. 9

Усложненная квадратурная формула Гаусса. 10

Правило Рунге практической оценки погрешности. 11

Уточнение приближенного решения по Ричардсону. 11

Особенности вычисления интегралов с помощью компьютера. 12

Порядок выполнения задания по лабораторной работе. 13

Основные определения

Общий принцип численного интегрирования истекает из определения интеграла: интеграл – предел последовательности частичных сумм функции, а также из геометрического значения: интеграл численно равен площади области, заключенной между осью Ох, пределами интегрирования и графиком функции.

Все методы численного интегрирования основаны на следующей теореме.

Обобщенная теорема о среднем

Пусть , причем . Тогда существует такая точка , что

                                                          

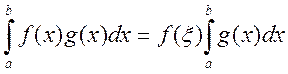
Теперь введем понятие квадратурной формулы. Пусть дан определенный интеграл

                                                                         

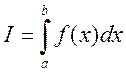
от  непрерывной на [a;b] функции f. Приближенное равенство

                                                                                                                       

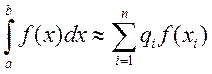
где  – некоторые числа,  – некоторые точки отрезка [a;b], называется квадратурной формулой, определяемой весами  и узлами .

Говорят, что квадратурная формула точна для многочленов степени m, если при замене f на произвольный алгебраический многочлен степени m приближенное равенство становится точным. Отсюда вытекает следующее определение.

Порядок точности ­–	максимальная степень многочлена, при которой аналитическая погрешность метода равна нулю.
Порядок аппроксимации –	Величина, характеризующая во сколько раз уменьшается погрешность метода при уменьшении шага. , где  ­– точное значение интеграла  ­– значение интеграла, вычисленное с шагом h

Каноническая формула прямоугольников

Допустим, что , . Положим приближенно

                                                                                            

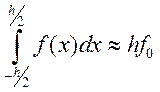
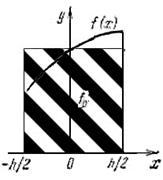где , то есть площадь криволинейной трапеции, ограниченной сверху графиком функции аппроксимируется площадью заштрихованного прямоугольника (см. рис. 1), высота которого равна значению f в средней точке основания трапеции.

Найдем теперь остаточный член, то есть погрешность формулы .

Рис. 1

Пусть

                                                                                     

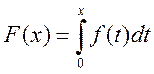
. Т.к. , то согласно формуле Тейлора с остаточным членом в форме Лагранжа имеем:

                                                                                       

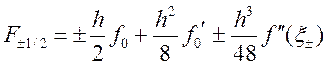
Где . Функция является первообразной , поэтому для интеграла, стоящего в левой части приближенного равенства из формулы Ньютона-Лейбница с учетом вытекает:

.

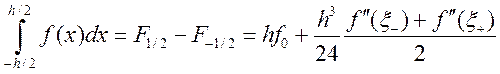            Отсюда вытекает выражения для формулы с остаточным членом.

                                                                           

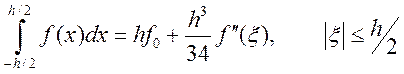
            Формула называется квадратурной формулой прямоугольников с остаточным членом.