Над полем действительных чисел можно вести следующие операции: сложение, вычитание, умножение и деление. Эти операции подчиняются следующим аксиомам:
I. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г)![]() .
.
II. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
III. ![]()
IV. Аксиомы порядка: ![]() иначе
иначе ![]()
V. Аксиомы непрерывности: ![]() и
выполняется неравенство
и
выполняется неравенство ![]() , то
всегда найдется такое число
, то
всегда найдется такое число ![]() , что
####### будут выполняться соотношения.
, что
####### будут выполняться соотношения.
Нетривиальным множеством, которое удовлетворяет вышеперечисленным аксиомам, называют множество действительных чисел.
![]() называется
ограниченным сверху (снизу), если
называется
ограниченным сверху (снизу), если ![]() такое, что
такое, что ![]() справедливо
неравенство
справедливо
неравенство ![]() (
(![]() ). Число
). Число ![]() называется
верхней (нижней) гранью множества
называется
верхней (нижней) гранью множества ![]() .
.
Множество, ограниченное сверху и снизу, называется ограниченным.
Наименьшее из чисел,
ограничивающих множество ![]() сверху,
называется точной верхней гранью множества
сверху,
называется точной верхней гранью множества ![]() :
: ![]() .
Число
.
Число ![]() называется супренумом множества
называется супренумом множества ![]() тогда и только тогда, когда 1.
тогда и только тогда, когда 1. ![]() ; 2.
; 2. ![]() ; 3.
; 3. ![]() .
.
Если ![]() , то его называют максимальным элементом
множества
, то его называют максимальным элементом
множества ![]() (
(![]() ).
).
Наибольшее из чисел,
ограничивающих множество ![]() снизу,
называется точной нижней гранью множества
снизу,
называется точной нижней гранью множества ![]() :
: ![]() .
. ![]() будет инфинумом множества
будет инфинумом множества ![]() тогда и только тогда, когда 1.
тогда и только тогда, когда 1. ![]() ; 2.
; 2. ![]() ; 3.
; 3. ![]() .
.
Верхней гранью
неограниченного сверху числового множества является ![]() , а нижней гранью -
, а нижней гранью - ![]() .
.
1. Любое ненулевое числовое
множество имеет верхнюю грань, принадлежащую расширенному множеству
действительных чисел. Если множество ограничено сверху, то верхняя грань
конечна, если не ограничено, то верхняя грань равна ![]() . 2. Аналогично для нижней грани.
. 2. Аналогично для нижней грани.
Принцип Архимеда. Каково бы ни было действительное число ![]() , существует такое
, существует такое ![]() , что
, что ![]() . Для
любых действительных чисел
. Для
любых действительных чисел ![]() и
и ![]() :
: ![]() , что
, что ![]() .
.
Принцип вложенных
отрезков. Система числовых отрезков ![]() называется системой вложенных отрезков, если все
границы этих отрезков упорядочены следующим образом
называется системой вложенных отрезков, если все
границы этих отрезков упорядочены следующим образом ![]() . Т.е. каждый следующий отрезок содержится в предыдущем
отрезке.
. Т.е. каждый следующий отрезок содержится в предыдущем
отрезке.
Принцип Коши-Кантора. Для всякой системы вложенных отрезков существует хотя
бы одно число, которое принадлежит всем отрезкам системы. Следствие: для всякой
системы вложенных отрезков, длина которых ![]() существует единственная точка
существует единственная точка ![]() , которая принадлежит всем отрезкам. Причем
, которая принадлежит всем отрезкам. Причем 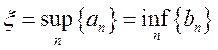 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.