








Задание №1
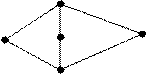 Проверить, что следующая диаграмма Хассе
определяет решетку. Будет ли эта решетка модулярной? Является ли она
дистрибутивной решеткой?
Проверить, что следующая диаграмма Хассе
определяет решетку. Будет ли эта решетка модулярной? Является ли она
дистрибутивной решеткой?
Решение:
Решеткой будем называть универсальную алгебру A=<А; s> сигнатуры s=<Ù, Ú>, удовлетворяющую условиям:
Для заданной универсальной алгебры A =<A, s>проверим аксиомы решетки:
xÙx=inf(x,x)=x
xÚx=sup(x,x)=x
xÙy=inf(x,y)=inf(y,x)=yÙx
xÚy=sup(x,y)=sup(y,x)=yÚx
(xÙy)Ùz=inf(inf(x,y), z)=inf(x,y,z)=inf(x, inf(y,z))=xÙ(yÙz)
(xÚy)Úz=sup(sup(x,y), z)=sup(x,y,z)=sup(x, sup(y,z))=xÚ(yÚz)
xÙ(xÚy)=inf(x, sup(x, y))=x
xÚ(xÙy)=sup(x, inf(x,y))=x
Так как данная универсальная алгебра удовлетворяет всем необходимым аксиомам, следовательно, она является решеткой.
Модулярной решеткой будем называть решетку A=<A; Ú, Ù>, удовлетворяющую условию:
"a,b,cÎA (aÙb)Ú(bÙc)=bÙ((aÙb)Úc) 1
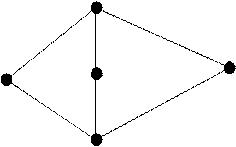 |
Пометим вершины искомой решетки:
a b c
0
1. Пусть x-произвольный элемент решетки, не равный 0 и 1. Для него справедливо:
(1Ù0)Ú(0Ùx)=0Ù((1Ù0)Úx)
![]()
![]() 0 Ú
0 = 0
0 Ú
0 = 0
0 = 0
Данное соотношение также справедливо для x=a, x=b, x=c.
2. Пусть x-произвольный элемент решетки, не равный 0 и 1. Для него справедливо:
(0Ù1)Ú(1Ùx)=1Ù((0Ù1)Úx)
![]()
![]() 0 Ú
x = 0
0 Ú
x = 0
x = x
Данное соотношение также справедливо для x=a, x=b, x=c.
3. Пусть x-произвольный элемент решетки, не равный 0 и 1. Для него справедливо:
(xÙ0)Ú(0Ù1)=0Ù((xÙ0)Ú1)
![]()
![]() 0 Ú
0 = 0
0 Ú
0 = 0
0 = 0
Данное соотношение также справедливо для x=a, x=b, x=c.
4. Пусть x-произвольный элемент решетки, не равный 0 и 1. Для него справедливо:
(xÙ1)Ú(1Ù0)=1Ù((xÙ1)Ú0)
![]()
![]() x Ú 0 = x
x Ú 0 = x
x = x
Данное соотношение также справедливо для x=a, x=b, x=c.
Так как данная решетка удовлетворяет всем необходимым аксиомам, следовательно, она модулярна.
Дистрибутивная решетка это любая решетка A=<A; Ú, Ù>, удовлетворяющая условию:
"a, b, cÎA aÙ(bÚc)=(aÙb)Ú(aÙc)
Теорема Дедекинда-Биркгофа.
Решетка A является модулярной тогда и только тогда, когда она не содержит подрешеток изоморфных решетке N. Решетка A является дистрибутивной тогда и только тогда, когда она не содержит подрешеток, изомофных решеткам N и M3.
 Где:
Где:
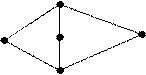 |
M3 N
В исходной решетке можно выделить подрешетку, изоморфную решетке M3, следовательно, данная решетка модулярна, но не является дистрибутивной.
Задание №2
Нарисуйте диаграмму Хассе решетки делителей числа 66. Образует ли эта решетка булеву алгебру? При утвердительном ответе определите число ее элементов.
Является ли эта универсальная алгебра простой?
|
|
|
|
|
|
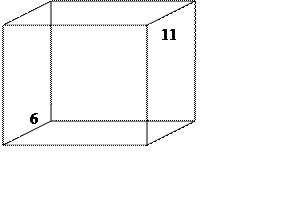 Диаграмма
Хассе решетки делителей числа 66
Диаграмма
Хассе решетки делителей числа 66
Булева алгебра это:
m=|M|, |Cm|=2m
(в общем случае – многомерные кубы являются конечными булевыми алгебрами)
В данном случае полученная диаграмма Хассе является трехмерным бинарным кубом, следовательно, искомая решетка образует булеву алгебру.
Теорема: Любая конечная булева алгебра изоморфна алгебре подмножеств ее атомов.
Конечная булева алгебра, в которой число атомов равно n изоморфна n- мерному кубу.
Атом решетки – минимальный ненулевой элемент. Элемент булевой алгебры a называется атомом, если a≠0 и для любого элемента алгебры b если b<a, то b=0.
В данной булевой алгебре атомами будут элементы: 3, 1 и 2.
Число атомов в данном случае 3 и мы получили 3х мерный куб. А количество элементов данной булевой алгебры равно восьми.
N = {{Æ},{1,2,3},{2},{1},{3},{2,3},{1,2},{1,3}}
Алгебру A назовем простой, если A неодноэлементна и ConA={DA, ÑA}, то есть любая конгруэнция алгебры A отличная от нулевой (от равенства) является единичной (тотальной) на A. Очевидно, что простота алгебры A эквивалентна равенству qa,b=ÑA для любых различных элементов a, b алгебры A.
Решетка делителей простых чисел, в данном случае числа 66, изоморфна решетке подгрупп группы вычетов целых чисел по модулю числа 66, а решетка подгрупп группы вычетов целых чисел по модулю числа 66, в свою очередь, изоморфна решетке конгруэнций этой группы.
Алгебра A простая, если Сon A ={DA, ÑA}.
Эта решетка состоит более чем из 2х элементов, так как число 66 не является простым. Из этого можно сделать вывод, что алгебра не является простой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.