Определение решетки диаграммы Хассе. Рисование диаграммы Хассе решетки делителей числа 14

Задание 1.

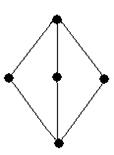
Проверить, что следующая диаграмма Хассе определяет решетку. Будет ли эта решетка модулярной? Является ли она дистрибутивной решеткой?

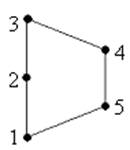
Решение:

Для того, чтобы определить является ли диаграмма Хассе решеткой, достаточно определить, для каждой пары элементов диаграммы inf и sup.

sup (1,2)=2 inf  (1,2)=1 sup (1,3)=3 inf  (1,3)=1 sup (1,4)=3 inf  (1,4)=1 sup (1,5)=5 inf  (1,5)=1

sup (2,3)=3 inf  (2,3)=2 sup (2,4)=3 inf  (2,4)=1 sup (2,5)=3 inf  (2,5)=1

sup (3,4)=3 inf  (3,4)=4 sup (3,5)=3 inf  (3,5)=1

sup (4,5)=4 inf  (4,5)=5

Таким образом, для всех пар определены inf и sup. Следовательно, рассматриваемая диаграмма Хассе –  решетка.

Условие модулярности:

Проверим, является ли модулярной данная решетка, рассмотрим вершины 2, 4, 5 :

.

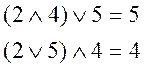
Дистрибутивной данная решетка не является, так как она не является модулярной.

Задание 2.

Нарисуйте диаграмму Хассе решетки делителей числа 14. Образует ли эта решетка булеву алгебру? При утвердительном ответе определите число её элементов. Является ли эта универсальная алгебра простой?

Решение:

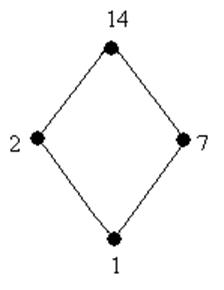- диаграмма решетки Хассе

Определим, образует ли решетка булеву алгебру. Для булевой алгебры необходимо выполнение следующих условий:

1) решетка дистрибутивна,

2)

      

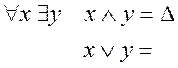
1) решетка дистрибутивна, так как она не содержит подрешетки вида:

      

2) x=14 y=1  

                               14V

     x=2  y=7  

                                V

     x=7  y=2  

                               V

     x=1  y=14  

                                 V

Значит, решетка образует булеву алгебру.

Построим решетку конгруэнции по следующему принципу:

      

      

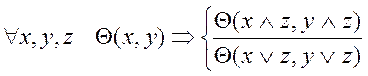
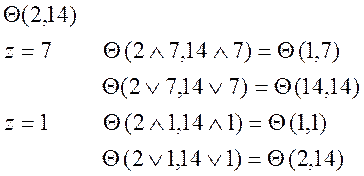
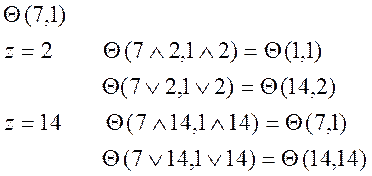
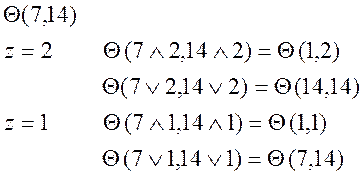
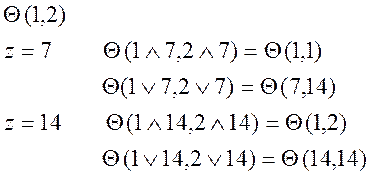
Заметим, что если , то этому же классу должны принадлежать и элементы 2 и 7, следовательно получаем .

Таким образом, решетка конгруентности имеет вид:

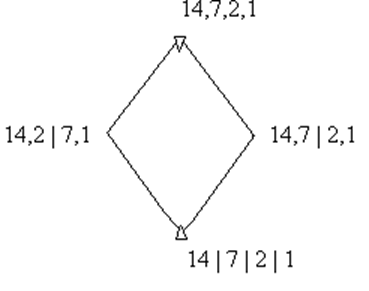
Для того, чтобы универсальная алгебра являлась простой, решетка конгруэнции должна содержать только экстремальные элементы. Следовательно, УА не является простой.

Задание 3.

Обозначим N = á,*ñ - универсальную алгебру натуральных чисел  с операцией произведения. Рассмотрим элементы 384 и 4374 этой алгебры и обозначим через В подалгебру порожденную этими двумя элементами.

Будет ли число 60466176 принадлежать этой подалгебре?

Решение:

Разложим число на множители:

60466176=384*4374*36

В разложении присутствует элемент меньше тех, что образуют подалгебру, а значит не принадлежит ей, следовательно, число 60466176 не являтся элементом подалгебры В.

Задание 4.

Рассмотрим группу вычетов Z₂₃₁ аддитивной группы целых чисел Z по модулю числа 231.

Определите решетку конгруэнции этой группы.

Является ли она простой?

Решение:

-группа вычетов целых чисел по модулю 33

B-подгруппа Z₃₃  

 …

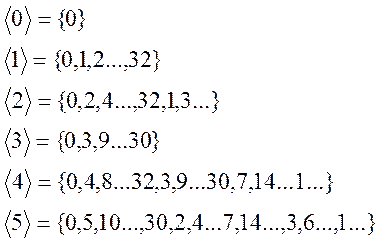
Заметим, что =

Получим следующую решетку:

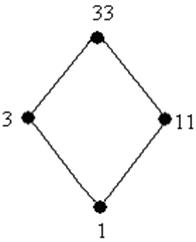
Решетка конгруэнции (см. задачу 2) имеет следующий вид:

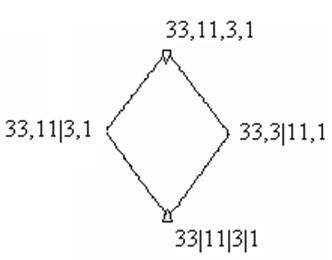
Так как решетка конгруэнции, помимо экстремальных элементов содержит и другие, то такая универсальная алгебра не является простой.

Задание 5.

Является ли универсальная алгебра Z₂₃₁ из предыдущей задачи пряморазложимой?

Решение:

   =                  .

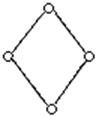
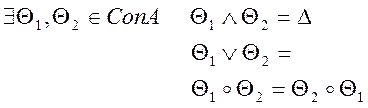
Следовательно, данная универсальная алгебра является прямо разложимой.            

Задание 6.

Образует ли многообразие следующая совокупность: групп вычетов целых чисел Z_n как класс универсальных алгебр?

Решение:

Нет, так как не выполняется аксиома принадлежности произведения группы вычетов классу.

Министерство образования и науки Российской Федерации

НГТУ

Кафедра   алгебры и математической логики

Типовой расчет

по дисциплине «Общая Алгебра»

Вариант 6

Факультет:           ПМИ

Группа:                 ПМ-51

Студенты:             Дворецкая Е.Н.

Преподаватель:  Давид Становски

Новосибирск

2007