Министерство образования и науки РФ
ГОУ ВПО
кафедра алгебры и математической логики
РГЗ по Общей Алгебре
Вариант 1
Факультет: ПМИ Преподаватели:
Группа: ПМ-56
Пономарев К.В.
Студент: Алестратова С.Е. Становски Д.
Новосибирск 2007
Задание 1
Проверить, что следующая диаграмма Хассе определяет решетку. Будет ли эта решетка модулярной? Является ли она дистрибутивной решеткой?

По теореме Дедекинда-Биркгофа решетка является модулярной тогда и только тогда, когда она не содержит подрешеток изоморфных N; решетка является дистрибутивной тогда и только тогда, когда она не содержит подрешеток, изоморфных решеткам N, M3. Где

![]()
![]()
![]() N : M3:
N : M3:
 |
Из теоремы решетка не является модулярной, так как она содержит подрешетку, изоморфную N. Данная решетка не дистрибутивная, так как она не модулярная.
Задание 2
Нарисуйте диаграмму Хассе решетки делителей числа 5. Образует ли эта решетка булеву алгебру? При утвердительном ответе определите число ее элементов.
Является ли эта универсальная алгебра простой?

Делители: 1,5
Решетка образует булеву алгебру, если элементы диаграммы можно разместить в n-мерном кубе.
Число элементов: 2
В данном случае, это одномерный куб, значит, решетка образует булеву алгебру.
Универсальная алгебра является простой. Так как кроме ![]() (x,y)
(x,y) ![]() x=y (самой маленькой конгруэнции) и
x=y (самой маленькой конгруэнции) и ![]() (x,y)
(x,y) ![]()
![]() x,y (самой грубой конгруэнции) не
существует других.
x,y (самой грубой конгруэнции) не
существует других.
Задание 3
Обозначим N = <N,·> - универсальную алгебру натуральных чисел с операцией произведения. Рассмотрим элементы 512 и 6561 этой алегебры и обозначим через B подалгебру, порожденную этими двумя элементами.
Будет ли число 120932352 принадлежать этой подалгебре?
B = <512α·6561β>
120932352 / 512=236196
236196 / 6561=36
36 не делится ни на 6561, ни на 512
Число 120932352 нельзя представить как произведение чисел 512α и 6561β
Значит, число 120932352 не принадлежит подалгебре B
Решение 2.
Определим вид элементов, порождаемых 6561 и 512 (т. е. подалгебру B). Разложим эти числа через простые делители.
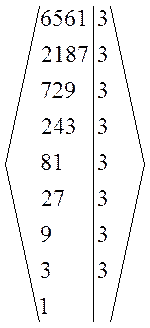
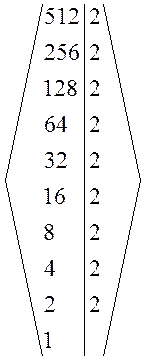
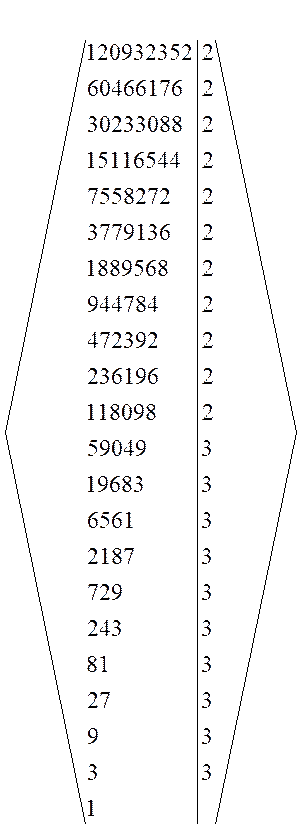
6561 = 38; 512 = 29; 120932352 = 211310.
Таким образом B =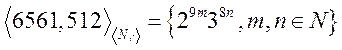
Число будет принадлежать этой подалгебре, если система будет иметь целые решения.
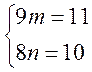
![]()
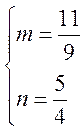
Решения не целые, значит, число 120932352 не принадлежит подалгебре B.
Задание 4
Рассмотрим группу вычетов ![]()
аддитивной группы целых чисел
аддитивной группы целых чисел ![]() по модулю числа 5.
Определите решетку конгруэнций этой группы.
по модулю числа 5.
Определите решетку конгруэнций этой группы.
Является ли такая универсальная алгебра простой?
Решетка конгруэнций совпадает с решеткой подалгебр.
Достаточно рассмотреть делители 5: 0,1
<0> = {0}
<1> = {0,1,2…..4}
Решетка конгруэнций:
Эта универсальная алгебра является простой.
Задание 5
Является ли универсальная алгебра ![]()
из предыдущей задачи прямо разложимой?
из предыдущей задачи прямо разложимой?
Алгебра является прямо разложимой, если существуют две
конгруэнции такие что: два нетривиальных элемента α и β (не![]() ,
,![]() ) удовлетворяют:
) удовлетворяют:
![]()
α ![]() β =
β = ![]()
α ![]() β =
β = ![]()
Универсальная алгебра ![]() не
является прямо разложимой, так как нет двух нетривиальных элементов α и β (не
не
является прямо разложимой, так как нет двух нетривиальных элементов α и β (не![]() ,
,![]() )
)
Задание 6
Образует ли многообразие совокупность простых универсальных алгебр.
Если все три свойства будут выполнены, то совокупность простых алгебр будет многообразием.
Алгебра является простой, если кроме ![]() (x,y)
(x,y) ![]() x=y (самой
маленькой конгруэнции) и
x=y (самой
маленькой конгруэнции) и ![]() (x,y)
(x,y) ![]()
![]() x,y (самой грубой конгруэнции) не
существует других.
x,y (самой грубой конгруэнции) не
существует других.
Заметим, что свойство 3. не выполняется. Приведем пример:
Возьмем две простых аглгебры.
Перемножим и получим решетку:
 |
Эта решетка не является простой, так как есть дополнительные
конгруэнции, отличные от ![]() (x,y) и
(x,y) и ![]() (x,y)
(x,y)
Значит, совокупность простых универсальных алгебр не является многообразием.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.