Проверка диаграммы Хассе на определение решётки. Рисование диаграммы Хассе решётки делителей числа «5»

Министерство Образования и Науки

Российской Федерации

Кафедра Алгебры и Математической Логики

Типовой расчёт по дисциплине

«Общая Алгебра»

Вариант №1

Факультет: ПМИ

Группа: ПМ-54

Студент: Брит С. В.

Преподаватель:  Давид Становски

Новосибирск 2007_г.

Задание №1____!

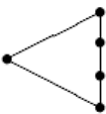Проверить, что следующая диаграмма Хассе определяет решётку. Будет ли эта решётка модулярной? Является ли она дистрибутивной решёткой?

Решение:

Для того, чтобы определить является ли диаграмма Хассе решеткой, достаточно определить, для каждой пары элементов диаграммы inf и sup.

sup(a,b)=b inf(a,b)=a	sup(b,c)=b inf(b,c)=c	sup(c,d)=c inf(c,d)=d	sup(d,e)=d inf(d,e)=e
sup(a,c)=b inf(a,c)=e	sup(b,d)=b inf(b,d)=d	sup(c,e)=c inf(c,e)=e
sup(a,d)=b inf(a,d)=e	sup(b,e)=b inf(b,e)=e
sup(a,e)=a inf(a,e)=e

Данная диаграмма Хассе является решёткой.  Кроме того, она содержит решётку, изоморфную N , следовательно, она не модулярная, а так как она не модулярна, то она не дистрибутивная.

-------------------------------------------------------------------------------------------------------------------------------------------------------------

Задание №2

Нарисуйте диаграмму Хассе решётки делителей числа «5». Образует ли эта решётка булеву алгебру? При утвердительном ответе определите число её элементов. Является ли эта универсальная алгебра простой?

Решение:

Диаграмма Хассе

Для булевой алгебры необходимо выполнение следующих условий:

1)  Решётка должна быть дистрибутивной.

2)   ;

;

1.  Решётка дистрибутивна, так как не содержит подрешёток М₃ и N .

2.   ;

 ;

 ;

 ;

Решётка образует булеву алгебру и содержит два элемента.

Алгебра является простой, так как возможно выделить только 2 конгруэнции: самая малая эквивалентность и самая грубая.

-------------------------------------------------------------------------------------------------------------------------------------------------

Задание №3

Обозначим   - универсальную алгебру натуральных чисел с операцией произведения. Рассмотрим элементы 512 и 6561 этой алгебры и обозначим через  подалгебру, порождённую этими двумя элементами. Будет ли число 120932352 принадлежать этой подалгебре?

Решение:

Разложим число на множители: 120932352 = 512 * 6561 * 36 ;

В разложении присутствует элемент, меньший элементов, образующих подалгебру, следовательно, данный элемент не принадлежит нашей подалгебре, как и число 120932352 .

-------------------------------------------------------------------------------------------------------------------------------------------------

Задание №4

Рассмотрим группу вычетов Z₅  аддитивной группы целых чисел Z по модулю числа 5. Определим решётку конгруэнции этой группы. Является ли такая универсальная алгебра простой?

Решение:

А = {1, 5};

Получим следующую решётку:

 

ConA=2 – данная алгебра является простой.

-------------------------------------------------------------------------------------------------------------------------------------------------

Задание №5

Является ли универсальная алгебра Z₅ из предыдущей задачи прямо разложимой?

Решение:

Алгебра является прямо разложимой, если существуют две конгруэнции такие что, два нетривиальных элемента α и β (не,) удовлетворяют:

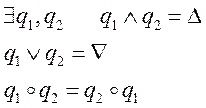
Данная универсальная алгебра не является прямо разложимой, так как нет двух нетривиальных элементов α и β.

-------------------------------------------------------------------------------------------------------------------------------------------------

Задание №6

Образует ли многообразие следующая совокупность: простых универсальных алгебр?

Решение:

1.  любая подалгебра алгебр из С принадлежит этому классу.

2.  любой гомеоморфный образ алгебры из класса С – алгебра класса  С

  3.   если А _I   алгебра класса С, то ПА _I   - алгебра класса С.

Совокупность простых универсальных алгебр не образует многообразия, так как не выполнится третье условие, а именно:

Перемножим две алгебры  и получим.                                                           Эта решетка не является простой, так как есть дополнительные конгруэнции, отличные от (x,y) и (x,y)

 ************************************************************************************************