Модулярная и дистрибутивная решетка заданной диаграммы Хассе. Рисование диаграммы Хассе решетки делителей числа 42

Задание  1.

Проверить, что следующая диаграмма Хассе определяет решетку. Будет ли эта решетка модулярной? Является ли она дистрибутивной решеткой?

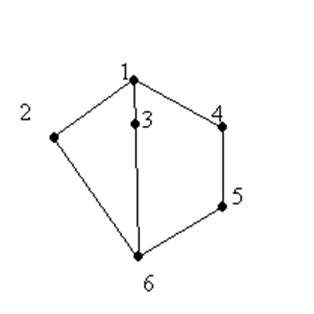
Решение.

Для проверки  того, что данная диаграмма является решеткой, проверим условие наличия sup и inf для каждой пары элементов данной решетки.

sup	1	2	3	4	5	6
1	1	1	1	1	1	1
2	1	2	1	1	1	2
3	1	1	3	1	1	3
4	1	1	1	4	4	4
5	1	1	1	4	5	5
6	1	2	3	4	5	6

inf	1	2	3	4	5	6
1	1	2	3	4	5	6
2	2	2	6	6	6	6
3	3	6	3	6	6	6
4	4	6	6	4	5	6
5	5	6	6	5	5	6
6	6	6	6	6	6	6

Так как для каждой пары элементов существует sup и inf, то даная диаграмма определяет решетку.

Эта решетка не является модулярной, покажем это. Для этого выпишем условие модулярности.

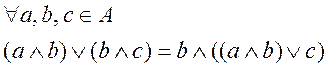
пусть a=5, b=4, c=2, тогда

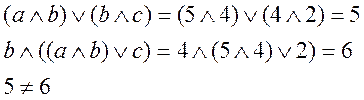
следовательно, решетка не модулярна. Так как любая дистрибутивная решетка является модулярной, то любая немодулярная решетка является недистрибутиной.

Задание 2.

Нарисуйте диаграмму Хассе решетки делителей числа 42. Образует ли эта решетка булеву алгебру? При утвердительном ответе определите число ее элементов.

Является ли эта алгебра простой?

Решение.

Нарисуем диаграмму Хассе решетки делителей 42.

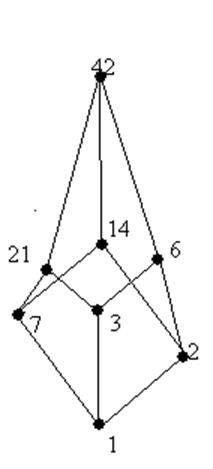
Эта решетка представляет собой трехмерный куб, следовательно, решетка делителей представляет собой булеву алгебру. В этой алгебре 8 элементов.

Для того, что бы доказать, что алгебра не является простой нужно показать конгруэнцию отличную от Ñ и D.  покажем ее:{14,7,21}, {2,3,6}, {1},{42}.

Задание 3.

Обозначим N = á,*ñ - универсальную алгебру натуральных чисел  с операцией произведения. Рассмотрим элементы 576 и 2946 этой алгебры и обозначим через В подалгебру порожденную этими двумя элементами.

Будет ли число 60466176 принадлежать этой подалгебре?

Решение.

Разложим число на множители:

60466176=104976*576=2916*36*576

60466176=2916*2916*7,1(1)

В обоих разложениях присутствуют элементы меньшие тех, что образуют подалгебру, а значит не принадлежащие ей – число 60466176 не являтся элементом подалгебры В.

Задание 4.

Рассмотрим группу вычетов Z₂₃₁ аддитивной группы целых чисел Z по модулю числа 231.

Определите решетку конгруэнции этой группы.

Является ли она простой?

Решение.

Для определения решетки конгруэнции данной группы вычетов определим решетку ее делителей и перевернем ее.

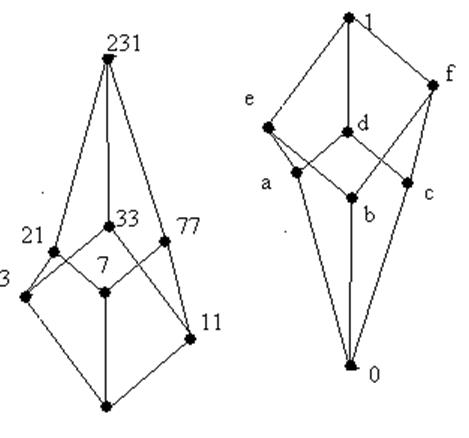
Данная универсальная алгебра не является простой, так как  существует конгруэнции:{c,f,b}, {e,a,d}, {1}, {0}.

Задание 5.

Является ли универсальная алгебра Z₂₃₁ из предыдущей задачи пряморазложимой?

Решение.

 Да, так как  существует два элемента e и c такие что sup(e,c)=1, inf(e,c)=0.

Задание 6.

Образует ли многообразие следующая совокупность: колец как класс универсальных алгебр?

Решение.

Да, так как класс алгебр выделяется универсальными условиями, и, следовательно, является многообразием.