Ток, охваченный контуром, 
, где N – число витков тороида.
Тогда в соответствии с законом полного тока
и
.
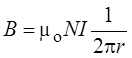Обратите внимание: магнитная индукция поля внутри тороида зависит от расстояния между центром тороида и точкой внутри него. Величина В обратно пропорциональна расстоянию r.
Можно показать, что поле вне тороида равно нулю (примерно так же, как это было сделано в предыдущем разделе для поля вне соленоида).
Рассмотрим произвольный замкнутый контур с током I. В соответствии с законом Био–Савара–Лапласа индукция магнитного поля, созданного контуром, прямо пропорциональна силе тока в проводнике.
Магнитный поток, охваченный
контуром, прямо пропорционален индукции магнитного поля внутри контура и его
площади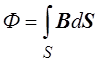 
.
Если охваченная контуром площадь неизменна, то величина магнитного потока прямо пропорциональна В и, следовательно, силе тока в контуре I
Ф = LI.
Коэффициент пропорциональности L называется коэффициентом индуктивности, или индуктивностью контура.
Индуктивность является размерным коэффициентом пропорциональности. В системе СИ размерность индуктивности [L] = Гн (генри).
Найдём выражение для расчёта индуктивности соленоида.
Как показано в разд. 3.11.1, магнитная индукция поля внутри соленоида В = mоnI.
Магнитный поток через один
виток соленоида Ф = mоnIS =
= 
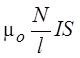, где l длина соленоида, N –
количество витков соленоида на длине l, S – площадь витка
соленоида.
Магнитный поток через N
витков соленоида равен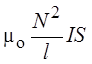 
.
Это означает, что для соленоида
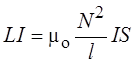
и отсюда индуктивность соленоида
,
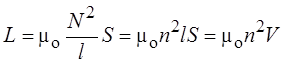где V – объём соленоида.
Таким образом, индуктивность соленоида без сердечника определяется плотностью витков и объёмом соленоида.
Магнитное поле создаётся электрическим током.
Если один ток создаёт магнитное поле в вакууме, а второй, такой же – в веществе, то созданные ими магнитные поля будут разными. Причём в некоторых веществах магнитное поле будет слабее поля в вакууме, в других – сильнее.
По соотношению поля в веществе и в вакууме вещества делят на три класса: диамагнетики, парамагнетики и ферромагнетики.
В данном разделе будут рассмотрены причины, по которым разные вещества намагничиваются по-разному.
Всякое вещество является магнетиком. Это значит, что всякое вещество способно намагничиваться, т. е. под действием внешнего магнитного поля в нём возникает дополнительное, собственное магнитное поле. Другими словами – индукция магнитного поля внутри магнетика В складывается из индукции внешнего поля Во и индукции собственного поля В¢:
В = Во+В¢.
Механизм намагничивания вещества был раскрыт французским учёным Андре Мари Ампером, который предположил, что во всех молекулах вещества циркулируют круговые токи. Каждый такой ток создаёт магнитное поле. Но, поскольку в отсутствие магнитного поля молекулярные токи ориентируются хаотически, суммарное магнитное поле всех этих токов равно нулю.
Появление внешнего магнитного поля вызывает упорядочение ориентации молекулярных круговых токов, в результате чего суммарное магнитное поле молекулярных токов становится отличным от нуля, а магнетик – намагниченным.
Намагничивание магнетика количественно характеризуют намагниченностью J, которая определяется выражением
,
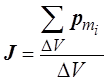где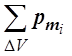 
– суммарный магнитный момент
всех молекул, находящихся в элементарном объёме DV в окрестности интересующей нас точки.
Размерность вектора намагниченности [J]
= [pm]/[V] =
А.м2/м3 = А/м.
|
|
Итак, намагничивание вещества есть результат упорядочивания ориентации молекулярных токов внешним магнитным полем. Условно это можно представить так, как показано на рисунке.
Как видно из рисунка, токи внутри объёма магнетика компенсируют друг друга.
Токи же, выходящие на боковую поверхность, компенсироваться не будут.
Поэтому намагничение вещества можно трактовать как результат появления на боковой поверхности магнетика макроскопического тока намагничивания I¢.
Пусть имеется магнетик, находящийся во внешнем магнитном поле.
Вычислим циркуляцию вектора магнитной индукции В по некоторому контуру L.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
