Расчёт магнитных полей с помощью закона Био–Савара–Лапласа. Магнитное поле в веществе (Главы 3-4 учебного пособия по общей физике), страница 2

Таким образом, индукция магнитного поля на оси кругового витка с током убывает обратно пропорционально третьей степени расстояния от центра витка до точки на оси. Вектор магнитной индукции на оси витка параллелен оси. Его направление можно определить с помощью правого винта: если направить правый винт параллельно оси витка и вращать его по направлению тока в витке, то направление поступательного движения винта покажет направление вектора магнитной индукции.

3.5  Силовые линии магнитного поля

Магнитное поле, как и электростатическое, удобно представлять в графической форме – с помощью силовых линий магнитного поля.

Силовая линия магнитного поля – это линия, касательная к которой в каждой точке совпадает с направлением вектора магнитной индукции.

Силовые линии магнитного поля проводят так, что их густота пропорциональна величине магнитной индукции: чем больше магнитная индукция в некоторой точке, тем больше густота силовых линий.

Таким образом, силовые линии магнитного поля имеют сходство с силовыми линиями электростатического поля.

Однако им свойственны и некоторые особенности.

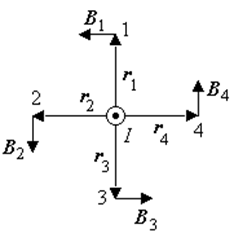
Рассмотрим магнитное поле, созданное прямым проводником с током I.

Пусть этот проводник перпендикулярен плоскости рисунка.

В различных точках, расположенных на одинаковых расстояниях от проводника, индукция одинакова по величине.

Направление вектора В в разных точках показано на рисунке.

Линией, касательная к которой во всех точках совпадает с направлением вектора магнитной индукции, является окружность.

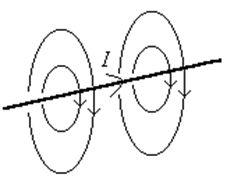Следовательно, силовые линии магнитного поля в этом случае представляют собой окружности, охватывающие проводник. Центры всех силовых линий расположены на проводнике.

Таким образом, силовые линии магнитного поля замкнуты (силовые линии электростатического не могут быть замкнуты, они начинаются и заканчиваются на зарядах).

Поэтому магнитное поле является вихревым (так называют поля, силовые линии которых замкнуты).

Замкнутость силовых линий означает ещё одну, очень важную особенность магнитного поля – в природе не существует (по крайней мере, пока не обнаружено) магнитных зарядов, которые являлись бы источником магнитного поля определённой полярности.

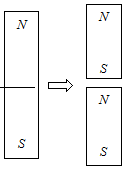
Поэтому не бывает отдельно существующе-го северного или южного магнитного полюса магнита.

Даже если распилить пополам постоянный магнит, то получится два магнита, каждый из которых имеет оба полюса.

3.6.  Сила Лоренца

Экспериментально установлено, что на заряд, движущийся в магнитном поле, действует сила. Эту силу принято называть силой Лоренца:

.

Модуль силы Лоренца

,

где a – угол между векторами v и B.

Направление силы Лоренца зависит от направления вектора . Его можно определить с помощью правила правого винта или правила левой руки. Но направление силы Лоренца не обязательно совпадает с направлением вектора !

Дело в том, что сила Лоренца равна результату произведения вектора [v, В] на скаляр q. Если заряд положительный, то F_л параллельна вектору [v, В]. Если же q < 0, то сила Лоренца противоположна направлению вектора [v, В] (см. рисунок).

Если заряженная частица движется параллельно силовым линиям магнитного поля, то угол a между векторами скорости и магнитной индукции равен нулю. Следовательно, сила Лоренца на такой заряд не действует (sin 0 = 0,  F_л = 0).

Если же заряд будет двигаться перпендикулярно силовым линиям магнитного поля, то угол a между векторами скорости и магнитной индукции равен 90⁰. В этом случае сила Лоренца имеет максимально возможное значение: F_л = qvB.

Сила Лоренца всегда перпендикулярна скорости движения заряда. Это означает, что сила Лоренца не может изменить величину скорости движения, но изменяет её направление.

Поэтому в однородном магнитном поле заряд, влетевший в магнитное поле перпендикулярно его силовым линиям, будет двигаться по окружности.

Если на заряд действует только сила Лоренца, то движение заряда подчиняется следующему уравнению, составленному на основе второго закона Ньютона: ma = F_л.

Поскольку сила Лоренца перпендикулярна скорости, постольку ускорение заряженной частицы является центростремительным (нормальным): 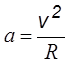 (здесь R – радиус кривизны траектории заряженной частицы).