Расчёт магнитных полей с помощью закона Био–Савара–Лапласа. Магнитное поле в веществе (Главы 3-4 учебного пособия по общей физике), страница 4

.

Векторный интеграл . Поэтому результирующая сила, действующая на контур, равна нулю.

Но это не означает, что равны нулю силы, действующие на отдельные участки контура. Например, на прямоугольный контур, плоскость которого перпендикулярна силовым линиям однородного магнитного поля, действуют растягивающие или сжимающие его силы (см. рисунок).

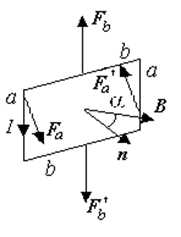Повернём контур так, чтобы положительная нормаль к его плоскости образовала некоторый угол a с силовыми линиями (направление положительной нормали определяют по правилу правого винта).

В этом случае на стороны b действуют силы, которые деформируют контур, но не вызывают его движения.

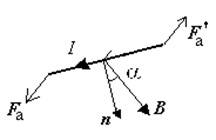Силы, действующие на стороны а контура, стремятся повернуть контур так, чтобы вектор n был параллелен вектору В (вектор n– единичный вектор, направление которого совпадает с положительной нормалью к контуру).

Модули этих сил равны F_a = IaB. Силы  и  создают момент пары сил, модуль которого равен

М = F_absina = IabB sina = IBSsina,

где S – площадь контура; a – угол между вектором F_a и продолжением стороны b контура; этот угол равен по величине углу между единичным вектором n и вектором В.

В векторной форме данное выражение имеет вид

.

где n – единичный вектор, направленный по положительной нормали к контуру.

Выражение для момента сил можно записать и в такой форме:

M = [p_m,B],

где p_m = ISn – магнитный момент контура с током; направление магнитного момента совпадает с положительной нормалью к контуру.

Из выражения для расчёта M следует, что величина момента сил зависит от ориентации контура в магнитном поле. Момент сил, действующий на контур максимален, если контур параллелен силовым линиям магнитного поля (при этом угол между магнитным моментом и вектором магнитной индукции равен 90⁰). Если же контур перпендикулярен им, то момент сил равен нулю.

Поэтому если магнитный момент p_m контура с током параллелен вектору В, то в однородном магнитном поле контур будет находиться в состоянии устойчивого равновесия.

Контур будет в равновесии и в том случае, когда a = 180⁰, но равновесие будет неустойчивым.

Следует отметить, что все выводы, сформулированные в данном разделе, верны и для контура произвольной формы, находящегося в однородном магнитном поле.

3.9.  Магнитный поток. Работа, совершаемая

при перемещении проводника с током

в магнитном поле

Рассмотрим контур из П-образного проводника и подвижной перемычки длиной l, находящийся в однородном магнитном поле.

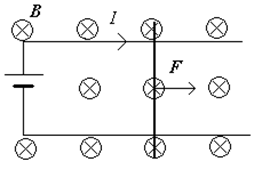Пусть в этом контуре источником ЭДС поддерживается постоянный ток I.

В результате взаимодействия с магнитным полем на перемычку будет действовать сила F = I [l, B]. Под действием этой силы перемычка будет двигаться вправо.

При смещении перемычки на dh сила F совершит работу dA = = Fdh = I[l, B]dh = IB[dh, l] = IBdS = IdФ, где dФ = BdS – магнитный поток через элементарную поверхность площадью dS.

Магнитным потоком называется скалярная величина, равная скалярному произведению вектора магнитной индукции на площадь элементарной поверхности dS, пронизываемой магнитным полем.

Из приведённых выше выкладок видно, что вектор элементарной поверхности dS = [dh, l] перпендикулярен поверхности dS и определяется по правилу правого винта для векторного произведения.

Размерность магнитного потока [Ф] = [B][dS] = Тл^.м² = Вб
(вебер).

Магнитный поток через конечную площадку S равен Ф.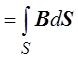

Таким образом работа, совершаемая при перемещении проводника с током в магнитном поле, определяется выражением

Ф

и равна произведению силы тока в проводнике на приращение магнитного потока, вызванное перемещением проводника.

В данном случае dФ есть поток вектора магнитной индукции через площадь, пройденную перемычкой в процессе её движения.

Теперь рассмотрим жёсткий замкнутый контур с током I, перемещающийся в магнитном поле.

Выделим бесконечно малый элемент контура dl. При его перемещении на расстояние dh магнитное поле совершает работу dА¢ = IdФ¢, где dА¢ – работа по перемещению элемента контура dl на расстояние dh, а dФ¢ – поток вектора магнитной индукции через площадь, пройденную элементом контура dl.

Работа по перемещению всего контура на dh

,

где dФ – магнитный поток через площадь, пройденную всеми элементами контура dl