Расчёт магнитных полей с помощью закона Био–Савара–Лапласа. Магнитное поле в веществе (Главы 3-4 учебного пособия по общей физике), страница 6

Поскольку соленоид симметричен относительно оси, проходящей через центры витков, постольку и созданное им магнитное поле должно быть симметричным относительно этой оси.

Следовательно, магнитное поле параллельно оси соленоида и в остальных точках, расположенных внутри соленоида.

Магнитное поле вне бесконечного соленоида равно нулю. Это можно доказать следующим образом.

_______________________

* Иногда этот закон называют теоремой о циркуляции вектора магнитной индукции.

Вначале допустим, что магнитное поле вне соленоида всё же существует.

Тогда оно должно быть симметричным относительно оси соленоида. Это значит, что силовые линии магнитного поля вне соленоида должны быть параллельны его оси.

Для определения индукции магнитного поля вне соленоида воспользуемся законом полного тока.

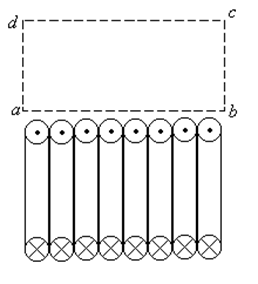
Найдём циркуляцию вектора магнитной индукции по прямоугольному контуру, у которого сторона ab проходит вдоль витков соленоида вблизи от них, а сторона cd находится бесконечно далеко от витков.

Скалярное произведение Bdl во всех точках сторон bc и da равно нулю, так как угол между В и dl на этих сторонах прямой.

Магнитное поле бесконечно далеко от соленоида равно нулю, поэтому вклад участка cd в циркуляцию также равен нулю.

Прежде чем определять вклад участка ab , найдём алгебраическую сумму токов, охваченных контуром abcd.

Поскольку контур не охватывает ни один виток соленоида, сумма токов равна нулю.

Следовательно, и циркуляция вектора В по контуру abcd должна быть равна нулю.

Но это означает, что и на участке ab скалярное произведение  равно нулю. Это возможно лишь в том случае, если индукция магнитного поля и вблизи от поверхности соленоида равна нулю.

Таким образом, магнитное поле вне бесконечно длинного соленоида действительно равно нулю.

Теперь найдём индукцию магнитного поля внутри соленоида.

В качестве контура интегрирования выберем прямоугольник 1234, две стороны которого параллельны оси соленоида, охватывающий несколько витков соленоида.

Циркуляция В по этому контуру равна

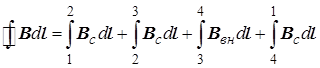
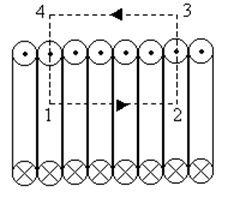На участках 2-3 и 4-1 индукция поля в соленоиде В_с перпендикулярна элементу контура dl, поэтому скалярное произведение В_с и dl равно нулю.

Интеграл на участке 3-4 также равен нулю, так как поле вне бесконечного соленоида равно нулю.

Следовательно, 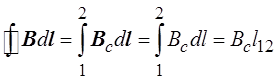, где l₁₂ – длина стороны 1-2 контура интегрирования.

При вычислении интеграла были учтены следующие соображения:

– внутри соленоида направление магнитной индукции и направление обхода контура совпадают, поэтому скалярное произведение Bdl равно произведению модулей этих векторов;

– модуль вектора магнитной индукции во всех точках участка контура 1-2 одинаков, поэтому В можно вынести за знак интеграла;

– интеграл 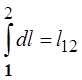, поэтому циркуляция равняется произведению модуля магнитной индукции на длину участка 1-2.

Ток, охваченный этим контуром, равен nl₁₂I, где n – количество витков на единице длины соленоида, I – ток в одном витке.

На основе закона полного тока циркуляция вектора магнитной индукции равна произведению m_о на алгебраическую сумму токов, охваченных контуром,

Bl₁₂ = m_onl₁₂I;

сокращая длину участка 1-2, получаем выражение для расчёта индукции магнитного поля внутри бесконечного соленоида:

B = m_onI.

Обратите внимание на то, что величина В внутри соленоида не зависит от расстояния между точкой и осью соленоида. Это значит, что магнитное поле внутри бесконечного соленоида однородно.

3.11.2.  Магнитное поле тороида

Тороидом называется соленоид, свёрнутый в кольцо.

Поскольку тороид симметричен относительно оси, проходящей через его центр перпендикулярно плоскости, в которой лежит тороид, то и магнитное поле должно быть симметрично относительно этой оси. Следовательно, силовые линии магнитного поля в тороиде также должны быть симметричны относительно той же самой оси.

В качестве контура интегрирования удобно выбрать окружность, совпадающую с какой-либо силовой линией магнитного поля.

В этом случае циркуляция вектора магнитной индукции  (направления В и dl во всех точках контура совпадают, поэтому скалярное произведение Bdl равно произведению их модулей; магнитная индукция во всех точках контура одинакова, следовательно, её можно вынести за знак интеграла).