Расчёт магнитных полей с помощью закона Био–Савара–Лапласа. Магнитное поле в веществе (Главы 3-4 учебного пособия по общей физике), страница 3

Используя выражение для расчёта ускорения и заменив F_л на qvB, получаем

.

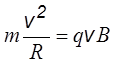Отсюда следует, что радиус окружности, по которой будет двигаться заряд в однородном магнитном поле, равен

.

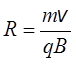Если заряженная частица влетит в однородное магнитное поле под углом a к силовым линиям, то её траектория будет более сложной.

Для того чтобы установить форму траектории и её параметры, разложим скорость частицы на две компоненты – параллельную v_|| = vcosa и перпендикулярную v_^= vsina силовым линиям магнитного поля.

Компонента скорости v_|| не изменяется, так как сила Лоренца не действует на заряженную частицу, движущуюся параллельно силовым линиям магнитного поля. За счёт этой компоненты заряд будет равномерно двигаться вдоль силовых линий.

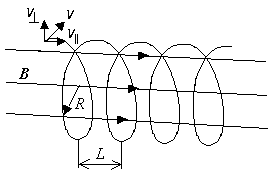Компонента скорости v_^ не будет меняться по величине, но будет непрерывно изменяться её направление. За счёт этой компоненты заряд будет двигаться по окружности, плоскость ко-торой перпендикулярна силовым линиям.

Заряженная частица одновременно будет участвовать в этих движениях, поэтому её траектория будет представлять собой винтовую линию.

Радиус винтовой линии будет равен .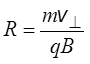

Период обращения заряженной частицы равен времени, за которое она пройдёт один виток, .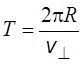

Шаг винтовой линии равен расстоянию, которое заряд пройдёт за один период: L = v_||T.

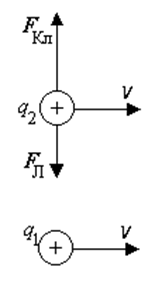
Рассмотрим два одноимённых заряда, движущихся с одинаковой скоростью v вдоль параллельных прямых.

За счёт кулоновского взаимодействия они отталкиваются с силой .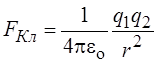

Каждый из зарядов создаёт магнитное поле. Следовательно, на заряды действует сила Лоренца.

Заряд q₁ создаёт магнитное поле, индукция которого направлена на нас (см. рисунок), и по модулю равна

.

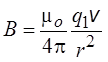Тогда сила Лоренца, действующая на второй заряд, по модулю равна

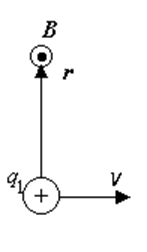
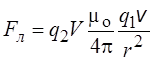
и направлена так, как показано на рисунке справа.

Отношение силы Лоренца к кулоновской силе равно

.

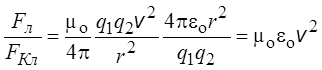Значения величин e_о и m_о связаны между собой соотношением 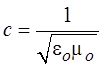, где с – скорость света в вакууме. Поэтому

.

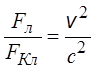Таким образом, в рассматриваемой ситуации сила Лоренца меньше кулоновской и возрастает по мере роста скорости движения заряда. Это ещё раз указывает на релятивистский характер магнитного взаимодействия.

3.7.  Сила Ампера

Если проводник с током поместить в магнитное поле, то на каждый электрон, направленно движущийся в проводнике, действует сила Лоренца.

Действие этой силы передаётся всему проводнику. В результате на проводник с током, находящийся в магнитном поле, будет действовать некоторая сила. Найдём её величину.

Для этого выделим элементарный участок проводника dl.
В нём имеется n.S.dl свободных электронов (n – концентрация свободных носителей заряда в проводнике, S – площадь поперечного сечения проводника, dl – длина элементарного участка). На каждый из электронов действует сила .

Результирующая сила dF, действующая на элемент проводника, равна сумме сил, действующих на все электроны в участке dl:

;

поскольку q.n.v = j, постольку сила dF равна

.

Это и есть выражение для расчёта силы Ампера, т. е. силы, действующей на элемент проводника с током, находящийся в магнитном поле.

Направление силы Ампера совпадает с направлением вектора  и может быть определено по правилу правого винта для векторного произведения (или по правилу левой руки).

Для вычисления силы, действующей на весь проводник, необходимо взять интеграл от dF по длине проводника:

.

Теперь рассмотрим два параллельных проводника с токами I₁ и I₂, расположенных на расстоянии b друг от друга.

Первый проводник создаёт магнитное поле, индукция которого

.

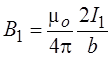В этом поле на единицу длины второго проводника действует сила, равная

.

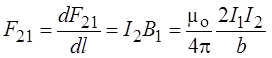Такая же по величине сила действует и на первый проводник. Легко увидеть, что если токи направлены в одну сторону, проводники притягиваются, если же токи противоположны, то проводники отталкиваются.

3.8.  Контур с током в однородном магнитном поле

Рассмотрим контур с постоянным током I, находящийся в однородном магнитном поле. На каждый элементарный участок контура действует сила Ампера .

Сила, действующая на контур в целом, равна сумме сил, действующих на все элементарные участки контура, и может быть выражена как

.

Учитывая, что I = const и в однородном магнитном поле В =
= const, величины I и В можно вынести за знак интеграла: