Признак монотонности функции. Алгоритм исследования функции

Признак монотонности функции. Для того, чтобы дифференцируемая на  функция  возрастала (убывала) необходимо и достаточно, чтобы во всех точках этого интервала , если всюду на этом отрезке производная строго больше или меньше нуля, то функция соответственно строго возрастает (строго убывает). Замечание: Эта теорема вена для функций, имеющих на некотором интервале конечное число точек, в которых производная не существует или равна нулю.

Пусть функция  определена в некоторой , тогда  называется точкой максимум (точкой минимума), если . Если верно строгое неравенство, то точка называется соответственно точкой строгого максимума или точкой строгого минимума. Точки (строгого) минимума (максимума) называются точками (строгого) экстремума.

Необходимое условие существования экстремума. Пусть  - точка экстремума функции , которая определена в некоторой . Тогда производная этой функции в данной точке либо не существует, либо равна нулю. Замечание: условие равенства нулю производной не является достаточным. Достаточное условие существования строгого экстремума. Пусть функция  дифференцируема в некоторой , кроме, быть может, самой точки , которая принадлежит . На этом интервале функция непрерывна. Если производная  меняет знак при переходе через точку , то точка  - точка строгого экстремума. При этом, если производная меняет знак с плюса на минус, то это точка строгого максимума, а если с минуса на плюс – строгого минимума.

Теорема. Пусть в точке  у функции  существуют производные до порядка  включительно, . Причем . Тогда если , то функция имеет в заданной точке строгий экстремум, а именно максимум при  и минимум при . Если же , то функция не имеет в заданной точке экстремума. В этом случае точка  является точкой возрастания, если  или точкой убывания, если . Следствия: 1) , то  - точка возрастания. Если , то точка убывания. 2) Если , то если вторая производная больше нуля, то  - точка строго минимума, меньше нуля – точка строго максимума. #COMMENT#

Точка, в которой либо производная не существует, либо равна нулю, причем функция определена в данной точке, называется критической.

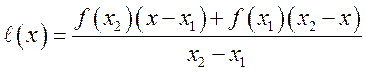. Функция  называется выпуклой вверх (вниз) на , если . Геометрическое определение выпуклости и вогнутости означает, что все точки хорды  лежит не выше (не ниже) точки графика функции , которая соответствует тоже аргументу . Всякий интервал, на котором функция (строго) выпукла вверх (вниз) называет интервалом (строгой)  выпуклости вверх (вниз).

Достаточное условие строгой выпуклости. Пусть функция  дважды дифференцируема на . Тогда если  на , то  строго выпукла вверх, а если , то  строго выпукла вниз. Замечание: Из теоремы следует, что условие выпуклости связано со знаком второй производной.

Теорема. Пусть функция  имеет на всем  положительную (отрицательную) вторую производную, тогда для  все точки  лежит выше (ниже) касательно в точке , где  принадлежит касательной.

Пусть функция  дифференцируема в точке . Пусть  - уравнение касательно к графику функции в точке . Если  меняет знак при переходе через точку , то эта точка называется точкой перегиба функции .

Необходимое условие существования точки перегиба. Если в точке перегиба существует , то она равна нулю. Замечание: Все точки перегиба функции – это точки, где вторая производная равна нулю или не существует. Достаточное условие существования точки перегиба. Если функция  дифференцируема в точке , дважды дифференцируема в некоторой проколотой  и вторая производная меняет знак при проходе через точку . То  - точка перегиба функции . Вторая достаточное условие существования точки перегиба. Пусть вторая производная в точке  равна нулю, а третья производная в этой точке не равна нулю, тогда  - это точка перегиба.

Пусть функция  определена. Если 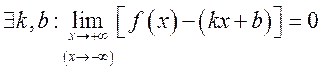, то  называется асимптотой графика функции . Замечание: Существование асимптоты означает, что при  функция ведет себя «почти как» линейная функция, т.е. отличается от линейной на бесконечно малую.

Пусть функция  определена в некоторой , может быть, даже односторонней. И пусть выполнено хотя бы одно из условий:  или . Тогда прямая  называется вертикальной асимптотой графика функции .

Алгоритм исследования функции. 1) Определить область существования функции, область непрерывности и точки разрыва. 2) Найти асимптоты. 3) Вычислить первую и вторую производную. 4) Определить точки, в которых первая и вторая производные либо не существуют, либо равны нулю. 5) Определить промежутки возрастания, убывания, выпуклости вверх и вниз для функции. Найти точки экстремума и точки перегиба.

Алгоритм исследования кривых заданных параметрически. 1) Найти множество  - общая часть области определения функций  и , отметив при этом значения параметра , включая , для которых хотя бы один из односторонних пределов равен  или . Эти точки могут быть асимптотами: а)  - вертикальная асимптота; б)  - горизонтальная асимптота; в)  - возможное существование наклонной асимптоты 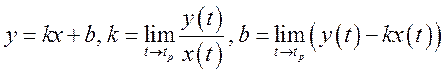. 2) Установить, обладает ли кривая симметрией: а)  - симметрия относительно ; б)  - относительно ; в)  - относительно начала координат; г)  - строится наложение двух графиков. 3) Найти нули функций  и , а также области знакопостоянства этих функций. 4) Найти точки , в которых хотя бы одна из производных равна нулю или разрывна. Тогда точки  (1, 4 пункты) разобьют все множество  на промежутки знакопостоянства функций . На каждом из  функция строго монотонна, следовательно можно определить на этом промежутке обратную функцию  и построить зависимость 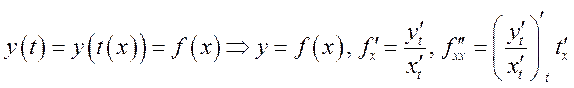. Часть кривой при  называется ветвью кривой. График этой кривой определяет зависимостью для . Если точка  и если на  производная  сохраняет знак, то тогда на этом интервале существует функция , для которой точки  являются точками возможного экстремума. Определить это можно, исследовав поведение функции на  и . 5) Найти  в которых . 6) Составить таблицу, первая строка которой содержит все промежутки из п.п. 1, 4, 5: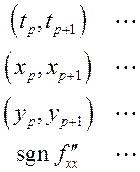 . 7)  Построить графики (по таблице) для каждой ветви кривой для .