Собственные интегралы. Признаки сходимости. Свойства равномерно сходящихся несобственных интегралов

  1.  Собственные интегралы, зависящие от параметра [2,5]

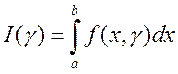Пусть в прямоугольнике  определена функция , интегрируемая по  на сегменте  при любом фиксированном . В этом случае на  определена функция , называемая интегралом, зависящим от параметра .

Теорема 1. Если  непрерывна в прямоугольнике , то функция :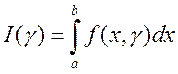

1) непрерывна на сегменте ;

2) интегрируема на сегменте  и справедливо равенство

.     

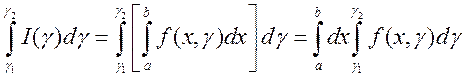41) Рассмотрим приращение 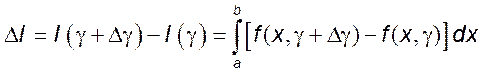. Для доказательства непрерывности функции  необходимо доказать, что  при . Так как функция  непрерывна на замкнутом множестве, то по теореме Кантора она равномерно непрерывна на нем. Следовательно,

.

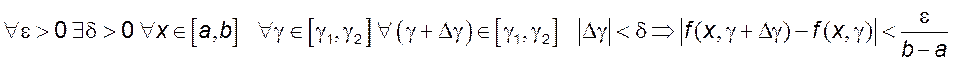Откуда по теореме о среднем получаем, что .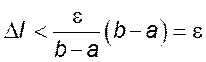

2) Так как функция  непрерывна на сегменте , то она интегрируема на этом сегменте, т.е. существует двойной интеграл . Следовательно, повторные интегралы (фигурирующих в соотношении ) равны, что доказывает справедливость формулы 3

Теорема 2. Если функция  и ее частная производная  непрерывны в прямоугольнике , то функция 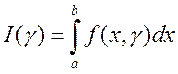 непрерывно дифференцируема на сегменте  и ее производная  может быть вычислена по правилу Лейбница .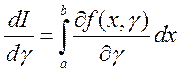

4Рассмотрим вспомогательную функцию 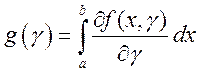. Так как  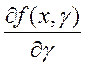непрерывна в прямоугольнике , то по предыдущей теореме  непрерывна на  и интеграл от функции  может быть найден по формуле .

, .

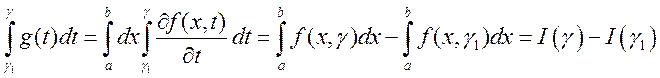Следовательно, 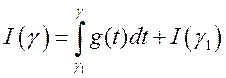. Производная от интеграла с переменным верхним пределом от непрерывной функции существует и равна значению этой функции в точке , поэтому

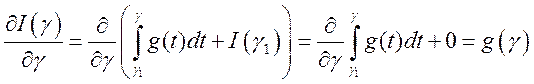.3

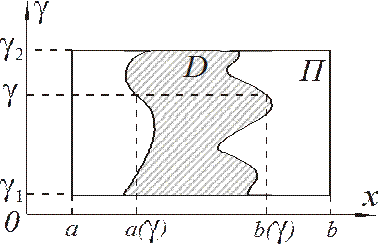Общий случай. Если при любом фиксированном  из сегмента  функция  интегрируема по  на сегменте , то на сегменте  определена функция

                          ,

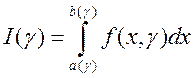представляющая собой интеграл, зависящий от параметра, у которого пределы интегрирования также зависят от параметра.

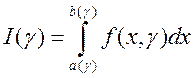Теорема 3. Пусть функция  непрерывна на прямоугольнике , а функции  и  непрерывны на сегменте . Тогда функция  непрерывна на сегменте .

4Пусть  – фиксировано. Представим  в следующей форме

.          

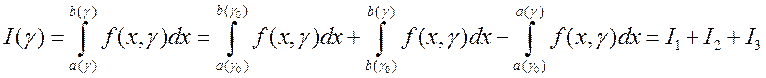Так как  – интеграл, зависящий от параметра , с постоянными пределами интегрирования и с непрерывной подынтегральной функцией, то в силу теоремы 1 этот интеграл является непрерывной функцией от  и поэтому при  стремится к .

Для интегралов  и  справедливы следующие оценки (теорема о среднем):

,        ,

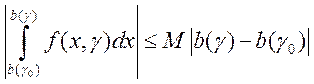где 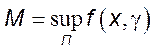. Так как функции  и  непрерывны на сегменте , то при   и , а значит и интегралы ,  также стремятся к 0. Таким образом, предел правой части при  существует и равен . Следовательно, функция  непрерывна в любой точке  сегмента .3

Следствие. Если , , то

.

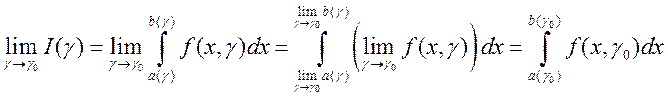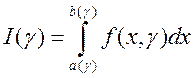Теорема 4. Пусть функция  и ее производная  непрерывны в прямоугольнике . Пусть далее функции  и  дифференцируемы на сегменте . Тогда функция  дифференцируема на сегменте , причем

.            

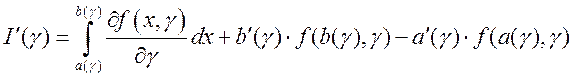4Пусть  – фиксировано. Представим  в виде .

 – интеграл, зависящий от параметра , с постоянными пределами интегрирования и с непрерывной подынтегральной функцией, поэтому, в силу теоремы 2, функция  дифференцируема на сегменте  и .

По определению производной для функции  получим .

По формуле среднего значения 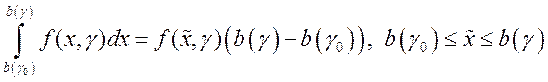. Из непрерывности функции  следует, что ; а из и дифференцируемости функции  следует, что 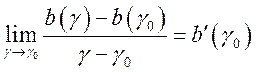. Поэтому

.

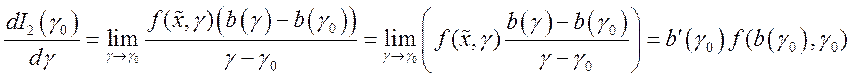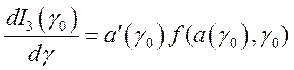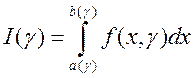Аналогично доказывается, что . Так как  произвольная точка сегмента , то можно утверждать, что функция  дифференцируема на сегменте  и ее производная может быть вычислена по формуле .3

\\\\\\\\\\\\\\\\\\\\\\\\\

  2.  Несобственные интегралы от ограниченных функций,
зависящие от параметра

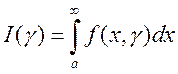Пусть в полуполосе  задана функция , интегрируемая по  в несобственном смысле на полупрямой  при любом фиксированном  из сегмента . При этих условиях на сегменте  определена функция , называемая несобственным интегралом первого рода, зависящим от параметра . При этом говорят, что интеграл сходится на сегменте .

Несобственный интеграл называется равномерно сходящимся по параметру  на сегменте , если он сходится на сегменте  и если  можно указать такое , зависящее только от , что   и  выполняется неравенство .

  2.1.  Признаки сходимости

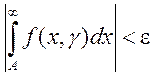Теорема 5 (критерий Коши). Для того, чтобы несобственный интеграл равномерно сходился по параметру  на сегменте , необходимо и достаточно, чтобы  можно было указать число , зависящее только от  и такое, что   и :

.

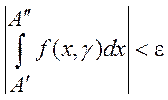Следствие. Несобственный интеграл 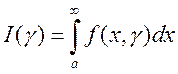,  сходится равномерно на сегменте , если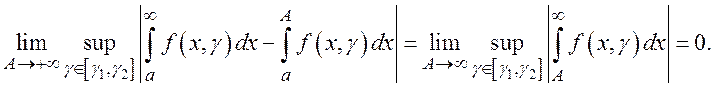

Теорема 6 (признак Вейерштрасса). Пусть функция  определена в полуполосе  и для каждого  из сегмента  интегрируема по  на любом сегменте . Пусть далее для всех точек полуполосы  выполняется неравенство , т.е.  равномерно ограничена на . Тогда из сходимости интеграла 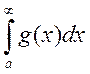 вытекает равномерная сходимость по  на сегменте  интеграла .

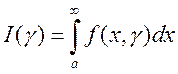4Так как , то 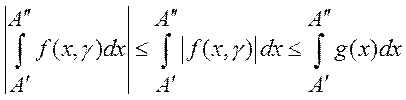. Из сходимости 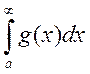 следует (по критерию Коши) равномерная сходимость интеграла .3

Следствие. Пусть функция , определенная в полуполосе , ограничена в этой полуполосе и при каждом  интегрируема по  на любом сегменте . Тогда, если сходится интеграл 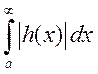, то сходится равномерно по  на сегменте  интеграл .

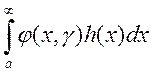Теорема 7. (Признаки Дирихле и Абеля).

Признак Дирихле	Признак Абеля
Пусть функции  и  определены в полуполосе . Несобственный интеграл  сходится равномерно на , если:
1) ;	1)  сходится равномерно на ;
2)   монотонна по ;
3)  при , т.е. .	3)  равномерно ограничена на , т.е. .

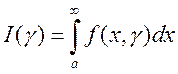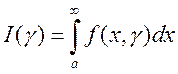Теорема 8 (Признак Дини). Пусть функция  непрерывна и неотрицательна в полуполосе , и пусть для каждого  сходится несобственный интеграл . Пусть далее функция  непрерывна на сегменте . Тогда интеграл  сходится  равномерно по  на этом сегменте.

Замечания.

1. Признаки Вейерштрасса, Дирихле и Абеля являются достаточными.

2. Для доказательства неравномерной сходимости обычно используют критерий Коши и его следствие.

3. Признак Вейерштрасса дает абсолютную сходимость. А признаки Дирихле и Абеля обычно используют при доказательстве условной сходимости.