4. Также как и в случае собственных интегралов,
зависящих от параметра, все вышесказанное (включая признаки сходимости)
обобщается на случай произвольного множества ![]() .
.
Теорема 9 (Предельный переход). Пусть ![]() ,
, ![]() ,
, ![]() – предельная точка множества
– предельная точка множества ![]() . Тогда, если
. Тогда, если
1) 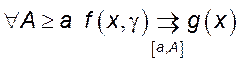 при
при ![]() ;
;
2) 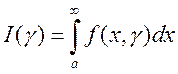 сходится равномерно на
сходится равномерно на
![]() ;
;
то 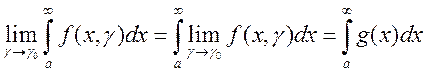 .
.
Замечание. ![]() может быть как
замкнутым, так и открытым множеством.
может быть как
замкнутым, так и открытым множеством.
Теорема 9 (Непрерывность). Пусть функция ![]() непрерывна в полуполосе
непрерывна в полуполосе ![]() , а интеграл
, а интеграл 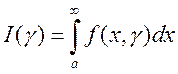 сходится
равномерно на
сходится
равномерно на ![]() . Тогда функция
. Тогда функция ![]() непрерывна на
непрерывна на ![]() .
.
Теорема 10 (Дифференцируемость). Пусть функция ![]() и ее частная производная
и ее частная производная ![]() непрерывны в полуполосе
непрерывны в полуполосе ![]() . Пусть далее для некоторого
. Пусть далее для некоторого ![]() из сегмента
из сегмента ![]() сходится
интеграл
сходится
интеграл 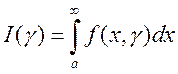 , а интеграл
, а интеграл 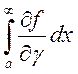 сходится
равномерно по
сходится
равномерно по ![]() на сегменте
на сегменте ![]() . При этих условиях функция
. При этих условиях функция ![]() дифференцируема на сегменте
дифференцируема на сегменте ![]() и
и 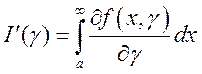 .
.
Теорема 11 (Интегрируемость). Если функция ![]() непрерывна в полуполосе
непрерывна в полуполосе ![]() , а интеграл
, а интеграл 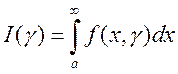 сходится
равномерно на сегменте
сходится
равномерно на сегменте ![]() , то интеграл
, то интеграл 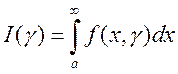 можно интегрировать по параметру
можно интегрировать по параметру ![]() на сегменте
на сегменте ![]() , причем
, причем
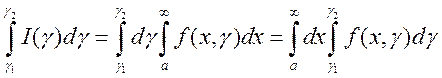 . (1)
. (1)
Следствие. Если функция ![]() непрерывна
и неотрицательна в полуполосе
непрерывна
и неотрицательна в полуполосе ![]() и интеграл
и интеграл 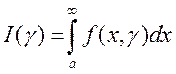 является непрерывной функцией на сегменте
является непрерывной функцией на сегменте ![]() , то справедлива формула (1).
, то справедлива формула (1).
Теорема 12 (Интегрируемость в несобственном смысле).
Пусть функция ![]() неотрицательна и
непрерывна при
неотрицательна и
непрерывна при ![]() и
и ![]() . Пусть
далее интегралы
. Пусть
далее интегралы 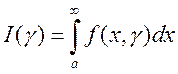 и
и 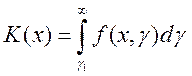 непрерывны
соответственно при
непрерывны
соответственно при ![]() и
и ![]() . Тогда
из сходимости одного из следующих двух несобственных интегралов:
. Тогда
из сходимости одного из следующих двух несобственных интегралов: 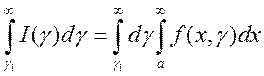 и
и 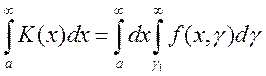 вытекает
сходимость другого и равенство этих интегралов.
вытекает
сходимость другого и равенство этих интегралов.
Теорема 13. Пусть функция ![]() удовлетворяет
условиям:
удовлетворяет
условиям:
1) ![]() ;
;
2) ![]()
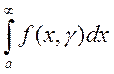 сходится
равномерно на
сходится
равномерно на ![]() ;
;
3) ![]()
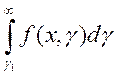 сходится
равномерно на
сходится
равномерно на ![]() ;
;
4) ![]() сходится интеграл
сходится интеграл 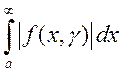 ;
;
5) ![]() сходится интеграл
сходится интеграл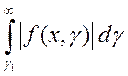 .
.
Тогда, если сходится хотя бы один из интегралов 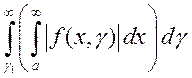 ,
, 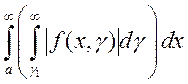 , то
справедливо равенство
, то
справедливо равенство 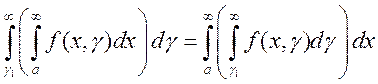 , в котором всех
интегралы сходятся.
, в котором всех
интегралы сходятся.
3. Несобственные интегралы от неограниченных функций, зависящие от параметра
Пусть функция ![]() задана в полуоткрытом
прямоугольнике
задана в полуоткрытом
прямоугольнике ![]() . Допустим, что при любом
фиксированном
. Допустим, что при любом
фиксированном ![]() несобственный интеграл второго
рода
несобственный интеграл второго
рода 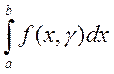 сходится. При этих условиях на сегменте
сходится. При этих условиях на сегменте ![]() определена функция
определена функция 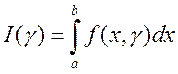 ,
называемая несобственным интегралом второго рода, зависящим от параметра
,
называемая несобственным интегралом второго рода, зависящим от параметра ![]() .
.
Несобственный интеграл 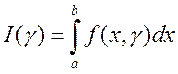 ,
, ![]() называется равномерно сходящимся по
параметру
называется равномерно сходящимся по
параметру ![]() , если он сходится
, если он сходится ![]() и
и ![]() можно
указать такое
можно
указать такое ![]() , зависящее только от
, зависящее только от ![]() , что
, что ![]()
![]() выполняется неравенство
выполняется неравенство 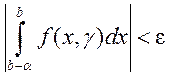 , или
, или
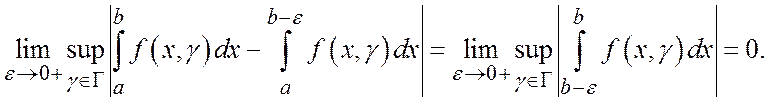
Замечание. Для несобственных интегралов второго рода
аналогично формулируются теоремы о непрерывности, интегрируемости и
дифференцируемости по параметру (так как несобственные интегралы второго рода с
помощью преобразования переменной ![]() сводятся к зависящим от
параметра несобственным интегралам первого рода.).
сводятся к зависящим от
параметра несобственным интегралам первого рода.).
Интегралы Эйлера
|
Бета-функция (интеграл Эйлера первого рода) |
Гамма-функция (интеграл Эйлера второго рода) |
|
|
|
|
Сходимость (область определения) |
|
|
|
|
|
Другие представления |
|
|
(подстановка
|
|
|
Связь
между интегралами Эйлера |
|
|
Непрерывна на всей области определения. |
|
|
Симметрична,
т.е. |
Положительна
|
|
Бесконечно дифференцируема, причем
|
|
|
|
|
|
Формулы приведения |
|
|
|
|
|
|
|
|
|
|
|
|
Формула дополнения
|
|
|
|
|
|
|
|
Формула удвоения Лежандра
|
|
|
Формула Стирлинга*
|
|
*Используется также для
приближенного вычисления ![]() при больших
при больших ![]() .
.
Докажем некоторые из приведенных выше свойств интегралов Эйлера [2].
Бета-функция 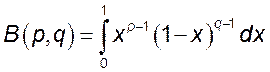
1. Сходимость
1. При ![]() и
и ![]() подынтегральная функция в соотношении непрерывна, поэтому интеграл в правой части является собственным. Следовательно, функция
подынтегральная функция в соотношении непрерывна, поэтому интеграл в правой части является собственным. Следовательно, функция ![]() определена для всех
определена для всех ![]() ,
, ![]() .
.
2. Пусть выполняются одно или оба из следующих неравенств ![]() ,
, ![]() .
.
В этом случае одна или обе из точек ![]() и
и
![]() являются особыми точками подынтегральной
функции. Представим функцию
являются особыми точками подынтегральной
функции. Представим функцию ![]() в виде
в виде
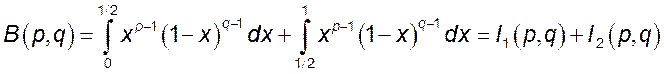 .
.
Для интеграла ![]() особой точкой будет
точка
особой точкой будет
точка ![]() . На сегменте
. На сегменте ![]() функция
функция
![]() непрерывна и поэтому ограничена некоторой
константой
непрерывна и поэтому ограничена некоторой
константой ![]() , тогда функция
, тогда функция ![]() будет
мажорантой для подынтегральной функции интеграла
будет
мажорантой для подынтегральной функции интеграла ![]() . Отсюда
следует, что интеграл
. Отсюда
следует, что интеграл ![]() сходится при
сходится при ![]() и любом
и любом ![]() . Аналогично
доказывается, что интеграл
. Аналогично
доказывается, что интеграл ![]() сходится при
сходится при ![]() и любом
и любом ![]() .
.
Объединяя случаи 1 и 2, получаем, что функция ![]() определена для
определена для ![]() .
.
2. Непрерывность
Для доказательства непрерывности ![]() в
квадранте
в
квадранте ![]() достаточно доказать равномерную сходимость
интеграла относительно параметров
достаточно доказать равномерную сходимость
интеграла относительно параметров ![]() и
и ![]() при
при ![]() и
и ![]() для
любы фиксированных значений
для
любы фиксированных значений ![]() и
и ![]() . При
. При ![]() справедливо
неравенство
справедливо
неравенство
![]() .
.
Отсюда их сходимости интеграла 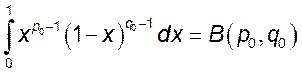 вытекает
в силу признака Вейерштрасса равномерная сходимость интеграла . Таким образом, непрерывность функции
вытекает
в силу признака Вейерштрасса равномерная сходимость интеграла . Таким образом, непрерывность функции ![]() в квадранте
в квадранте ![]() доказана.
доказана.
3. Формулы приведения
Считая, что ![]() , интегрируем по частям
функцию
, интегрируем по частям
функцию ![]()
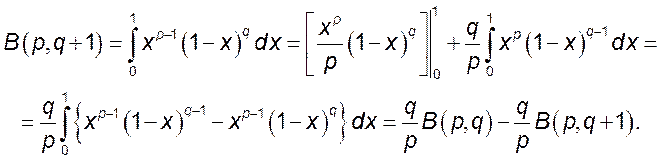
Следовательно, 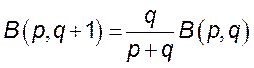 .
.
Учитывая симметрию функции ![]() ,
получаем вторую формулу приведения
,
получаем вторую формулу приведения 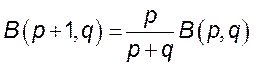 .
.
Гамма-функция 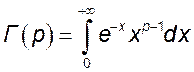
1. Сходимость
Представим функцию ![]() в
виде
в
виде 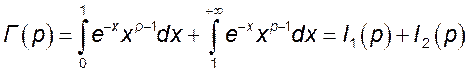 .
.
1. Так как ![]() при
при ![]() , а
, а 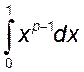 сходится
при
сходится
при ![]() , то и интеграл
, то и интеграл ![]() сходится
при
сходится
при ![]() (по признаку Вейерштрасса).
(по признаку Вейерштрасса).
2. Так как ![]() при любом
при любом ![]() , то из сходимости интеграла
, то из сходимости интеграла 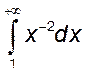 следует сходимость интеграла
следует сходимость интеграла ![]() при любом
при любом ![]() . (Из
определения предела
. (Из
определения предела 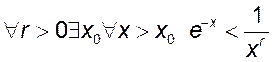 , следовательно
, следовательно 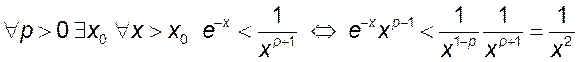 ).
).
2. Непрерывность
Для доказательства непрерывности ![]() на
полупрямой
на
полупрямой ![]() , достаточно установить равномерную
сходимость интеграла относительно параметра
, достаточно установить равномерную
сходимость интеграла относительно параметра ![]() при
при ![]() для
любых фиксированных значений
для
любых фиксированных значений ![]() и
и ![]() , удовлетворяющих условию
, удовлетворяющих условию ![]() .
.
При ![]() степенная функция убывает,
поэтому
степенная функция убывает,
поэтому ![]() (т.к.
(т.к. ![]() ),
),
а при ![]() степенная
функция возрастает, поэтому
степенная
функция возрастает, поэтому ![]() . Поэтому,
. Поэтому, ![]() справедливы неравенства
справедливы неравенства 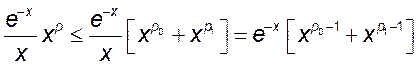 .
.
Равномерная сходимость интеграла ![]() следует
в силу признака Вейерштрасса из сходимости интеграла
следует
в силу признака Вейерштрасса из сходимости интеграла 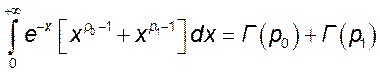 .
.
3. Формула приведения
Применяя формулу интегрирования по частям для функции ![]() при
при ![]() получим
получим
 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.