Термодинамика: теплоемкость, адиабатический и политропический процессы, страница 7

.

В полученное уравнение входят все три параметра: р, V и Т. Один из них можно исключить с помощью уравнения состояния. Чтобы получить уравнение политропы сразу в переменных р и V, исклю­чим Т. Для этого продифференцируем уравнение Менделеева -Клапейрона pV = RT:

.

Тогда  или

Согласно уравнению  Майера , тогда, разделив переменные, получаем

Величины  являются постоянными. Поэтому после интегри­рования получаем

Разделив это соотношение на  (что возможно, если сс_v) и произведя потенцирование, получим

                                                              (5.10)

где                                                                                                                              (4.11)    

Это и есть искомое уравнение политропы идеаль­ного газа для случая, когда сс_v. Величина п называется показателем политропы.

Чтобы установить характер политропического процесса при с = с_v, обратимся к уравнению (5.10). При с = с_v  это уравне­ние принимает вид (с − с_p) ln V = const, откуда следует, что V в ходе процесса остается постоянным. Таким образом, политропи­ческий процесс с теплоемкостью с = с_v является изохорическим процессом. Это можно было предвидеть заранее, поскольку  с_v = const и пред­ставляет собой теплоемкость при постоянном объеме, т. е. при изохорическом процессе. Согласно (5.11) по­казатель политропы при изохорическом процессе равен бесконечности.

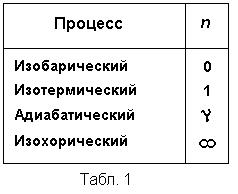
Остальные рассмотренные в предыду­щем параграфе процессы также относятся к категории политропических процессов. Изобарическому процессу соответствует n = 0, изотермическому — n = 1 и, наконец, адиабатическому — n = γ. Значения показателя политропы n для перечисленных процессов даны в табл1.

Решив уравнение (5.11) относительно с,  получим формулу для теплоемкости идеального газа при политропическом процессе:

.

Подстановка n = γ обращает это выражение  в нуль

.

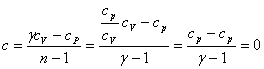 Следовательно, теплоемкость идеального газа при адиа­батическом процессе равна нулю. При адиабатическом процессе теплоемкость равна нулю для всех тел. Это вытекает из того, что при адиабатическом процессе d'Q = 0, в то время как  изменение температуры  dT  отлично от нуля.

При n = 1

Таким образом, при изотермическом процессе теплоемкость бес­конечно велика. Это объясняется тем, что при изотермическом про­цессе dT = 0, в то время как теплота d'Q отлична от нуля.

5.5.Работа, совершаемая идеальным газом при изопроцессах