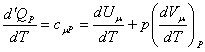Термодинамика: теплоемкость, адиабатический и политропический процессы, страница 6

.

Тогда

.

Однако из уравнение Менделеева  - Клапейрона  получаем .  Поэтому

 .                                     ( 5.8)

Таким образом,  универсальная газовая постоянная численно равна работе, которую совершает моль идеального газа при повышении его температуры на один Кельвин при постоянном давлении.

              Уравнение  (5.8) выражает связь изобарной и изохорной теплоемкостей и называется уравнением Майера.

            Далее под теплоемкостью мы будем понимать только молярную теплоемкость, поэтому индекс  писать не будем.

        Обозначим . Тогда ,  и

 .             

Для одноатомных газов . Для двухатомных газов

5.3.Адиабатический процесс

              Адиабатическим (адиабатным ) называется процесс, происходящий без теплообмена с внешней средой. Рассмотрим поведение идеального газа при адиабатическом процессе.

Из первого начали термодинамики имеем  , для адиабатического процесса d^/Q=0 , поэтому

 Из уравнения состояния идеального газа выразим давление , поэтому

, или    Проинтегрируем, получим:

,

Но , поэтому 

– уравнение адиабаты в переменных T и V.

Если подставить  Т из уравнения Менделеева  - Клапейрона,  , то получим:

                                                                        (5.9)

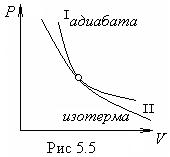 – уравнение адиабатного процесса или уравнение адиабаты в переменных р и V.  Уравнение изотермы в тех же переменных pV=const.  Постоянная g называется коэффициентом  Пуассона.

Покажем, что адиабата (5.9) идет круче изотермы. Для этого сравним производные dp/dV для обоих процессов. Для изотермического процесса

,

откуда

.

Для    адиабатного    процесса , откуда

.                

Поскольку , то адиабаты, дейст­вительно, идут круче изотерм  (рис.5.5).

5.4.Политропические процессы

Политропическими (политропными) называются процессы, при кото­рых теплоемкость тела остается постоянной. Таким образом, условие, которое выполняется в ходе политропического процесса, заключается в том, что .

Найдем уравнение политропы для идеального газа. Напишем уравнение первого начала термодинамики (для одного моля газа)