Термодинамика: теплоемкость, адиабатический и политропический процессы, страница 2

            Квазистатический процесс легко представить, если реальная скорость процесса  много меньше  скорости восстановления равновесия. В этом случае при реальных изменениях с малой скоростью равновесие восстанавливается с большой скоростью, и при  реальном изменении состояния макроскопической системы эта система проходит через ряд равновесных состояний.

          Рассмотрим макроскопическую систему А, взаимодействующую с термостатом В. Будем считать  давление макроскопической системы А равным  р, а давление термостата (р+). Тогда за счет бесконечно малого перепада давление начинается процесс выравнивания давления - система А начинает сжиматься. Если бы переход давления был равен нулю, то процесс отсутствовал бы, и его скорость  была бы равна нулю. При бесконечно малом перепаде скорость процесс бесконечно мала, а скорость  процесса восстановленного равновесия в газе конечна, т.е. , и процесс сжатия газа будет проходить через последовательность равновесных состояний, т.е. квазистатически.

         Такой процесс называют обратимым, т.к. достаточно бесконечно малых условий, и процесс потечет в обратном направлении, то есть если давление газа будет p+, а термостата р, то газ будет расширяться, проходя квазистатически через те же  состояния, но в обратном порядке.

          В термодинамике обратимыми процессами называют такие процессы, которые могут протекать как в прямом, так в обратном направлениях без заметных (конечных) изменений в окружающей среде. Если же скорость протекания процесса много больше скорости восстановления равновесия, , то процесс называется нестатическим или неравновесным. В этом случае   система проходит ряд неравновесных состояний. Физически такая ситуация встречается тогда, когда имеет место конечный перепад (градиент) параметров системы А и термостата В. Такие процессы называют еще необратимыми, т.к.  бесконечно малых изменений  условий в конечном состоянии будет недостаточно, чтобы вернуть систему в исходное состояние, т.е. процесс нельзя обратить без конечных изменений в окружающей среде.

           3.Полное изменение энергии равновесной системы. Рассмотрим систему А, которая находится в состоянии равновесия. Полное изменение средней энергии системы определяется выражением:

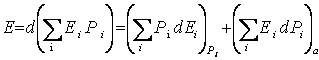.                              (5.2)

Первое слагаемое в  выражении (5.2) -  это работа , совершаемая над системой. Второе слагаемое - это та часть изменения энергии макроскопической системы, находящейся во взаимодействии с термостатом, которая не связана с изменением внешних параметров (а=const). Это вклад в изменение средней энергии системы за счет непрерывной передачи энергии от частиц термостата В к частицам  системы А. Если внешние параметры не меняются, то энергия отдельных микросостояний не меняется, и энергия, подводимая к макроскопической системе извне, идет на изменение распределения вероятностей. Состояние с большей энергией становятся более вероятными - система нагревается. Эту часть изменения полной энергии называют теплотой dQ. Итак, имеем:

.                                                      (5.3)

Знаки в уравнении (5.3) определим следующим образом. Энергию, полученную системой А, будем считать положительной, а отдаваемую - отрицательной. Если dQ>0 - система получает теплоту (эндотермический процесс). Если dQ<0 - система отдает теплоту  (экзотермический процесс).