Термодинамика: теплоемкость, адиабатический и политропический процессы, страница 4

          Все эти вопросы были разрешены в рамках квантовой механики. Известно, что вращательная и колебательная энергии молекулы квантованы. Их уровни энергии

где r – вращательное квантовое число (r=0,1,2,3…),  - колебательное квантовое число,         ( =0,1,2,3…),  - момент инерции молекулы относительно той или иной главной оси,  - собственная частота колебаний,  - постоянная Планка.

           Минимальная вращательная энергия молекулы водорода, рассчитанная по этим формулам, составляет порядка 0,01эВ, при низких температурах  (~50К) средняя энергия поступательного движения молекулы вдвое меньше минимальной вращательной энергии, т.е. ее оказывается недостаточно, чтобы возбудить вращательные степени свободы. В этих условиях говорят, что вращательные степени свободы  «заморожены».

           В области температур ~500К вращательные степени свободы полностью разморожены, и молекула водорода ведет себя как жесткая двухатомная молекула с числом степеней свобода 5=3+2.  При этом включаются две, а не три  вращательные степени свободы, Это связано с тем, что для включения степени свободы, соответствующей вращению молекулы вокруг ее оси, проходящей через оба ядра, требуется значительно большая энергия из-за малости момента инерции молекулы относительно этой оси.

            При температурах, превышающих 1000К, энергии уже оказывается достаточно для постепенного возбуждения колебательной степени свободы.

Обычно вместо работы , совершаемой внешними телами над системой, рассматривают работу  , совершаемую системой над внешними телами. Очевидно, , тогда первое начало термодинамики принимает вид:

                                                                     (5.6)

- количество теплоты, сообщенной системе, идет на приращение внутренней энергии системы и совершение системой работы над внешними телами.

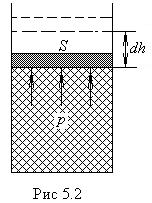
             Найдем работу, совершаемая макросистемой. Если объем макроси­стемы (например, газа) получает приращение dV, а давление, оказываемое ею на соседние тела (стенки), равно р, то элемен­тарная работа сил, действующих со стороны газа на стенки, равна  . Это легко получить для случая, когда систе­ма (газ) находится в цилиндре с поршнем (рис.5.2.)

             Элементарная работа, совершае­мая газом при перемещении поршня на , равна , где F — сила, с которой газ действует на поршень. Площадь сечения по­следнего S, поэтому F = pS и  , где . Отсюда .

             При поднятии поршня давление газа, вообще говоря, может меняться. Поэтому работа, совершаемая газом при конечных изменениях объема, например от до V₂, должна быть представле­на в виде интеграла:

                                 A=pdV .                                             (5.7)