Интеграл Римана (Определенный интеграл)
Основные определения. Интегральные суммы
Определение. Пусть![]() . Разбиением
. Разбиением ![]() называется такое множество
называется такое множество![]() .
.
Определение. Любой отрезок вида ![]() называется
подотрезком разбиения.
называется
подотрезком разбиения.
Определение. ![]() - длина
- длина ![]() -ого подотрезка разбиения.
-ого подотрезка разбиения.
Определение. Мелкостью
разбиения ![]() называется
минимальная из всех длин подотрезков этого разбиения
называется
минимальная из всех длин подотрезков этого разбиения![]() . Т.к.
множество подотрезков конечно, то эта величина всегда имеет смысл, а т.к. среди
. Т.к.
множество подотрезков конечно, то эта величина всегда имеет смысл, а т.к. среди
![]() нет совпадающих, то величина всегда больше
нуля.
нет совпадающих, то величина всегда больше
нуля.
Определение.![]() .
.
Определение. Нижней
интегральной суммой Дарбу называет
выражение![]() . Верхней интегральной суммой
называют
. Верхней интегральной суммой
называют![]() .
.
Следствие.![]() .
.
Определение. На каждом ![]() выберем
выберем![]() , а совокупность всех этих точек обозначим
, а совокупность всех этих точек обозначим![]() . Назовем ее выборкой и составим интегральную
сумму Дарбу:
. Назовем ее выборкой и составим интегральную
сумму Дарбу:![]() .
.
Следствие.![]() .
.
Определение. Говорят, что разбиение ![]() вписано
в разбиение
вписано
в разбиение ![]() (
(![]() ), если
множество точек
), если
множество точек![]() , образующих
, образующих![]() , содержит в себе множество точек
, содержит в себе множество точек![]() , образующих
, образующих![]() .
.
Замечания:
1)
![]() ;
;
2)
![]() .
.
Свойства интегральных сумм
1)
Если функция ![]() ограничена на
ограничена на![]() , то при
любом выборе
, то при
любом выборе ![]() верхняя и нижняя интегральные суммы
существуют. Это следует из того, что в силу ограниченности функции ее инфимум и
супремум каждого из подотрезков будут выражаться конечными числами, а,
следовательно, все слагаемые в интегральных суммах имеют смысл.
верхняя и нижняя интегральные суммы
существуют. Это следует из того, что в силу ограниченности функции ее инфимум и
супремум каждого из подотрезков будут выражаться конечными числами, а,
следовательно, все слагаемые в интегральных суммах имеют смысл.
1)
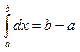 ;
;
2)
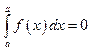 ;
;
3)
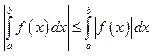 ;
;
4)
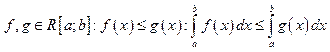 ;
;
5)
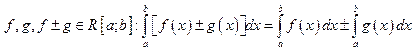 ;
;
6)
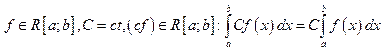 ;
;
7)
Теорема о среднем.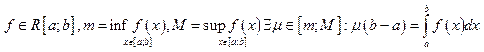 ,
где
,
где ![]() называют средним значением функции
на отрезке.
называют средним значением функции
на отрезке.
8)
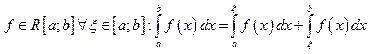 .
.
Интеграл Римана, как функция верхнего предела
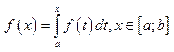
Теорема.![]() .
.
Доказательство. Пусть![]() . Чтобы показать
. Чтобы показать![]() , покажем
, покажем![]() . Для
этого
. Для
этого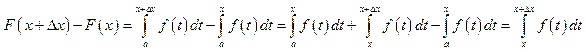 . Т.к.
. Т.к.![]() , то
, то ![]() ограничена на
ограничена на![]() .
Рассмотрим
.
Рассмотрим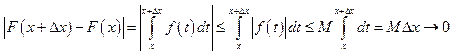 .
.
Теорема. Если![]() , то
, то ![]() является дифференцируемой в точке
является дифференцируемой в точке![]() , причем
, причем![]() .
.
Теорема. Любая непрерывная на отрезке функция ![]() имеет на этом отрезке первообразную
имеет на этом отрезке первообразную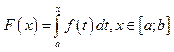 .
.
Доказательство. 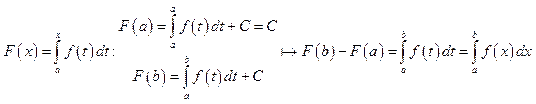 - Формула
Ньютона-Лейбница.
- Формула
Ньютона-Лейбница.
Теорема. Пусть выполняются 3 условия:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ,
,
то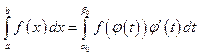 .
.
Доказательство. Поскольку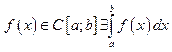 , т.к.
, т.к.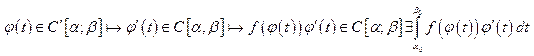 . Покажем равенство интегралов:
. Покажем равенство интегралов: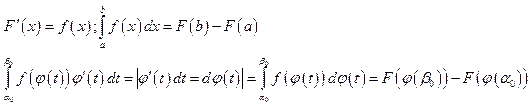 ,
,
т.к.![]() .
.
Теорема об интегрировании
по частям. Пусть функции![]() , тогда имеет место формула:
, тогда имеет место формула: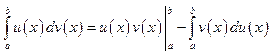 .
.
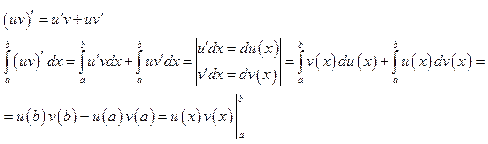 .
.
Некоторые интегральные неравенства:
1)
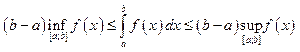 ;
;
2)
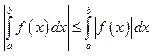 ;
;
3)
Неравенство Коши-Буняковского.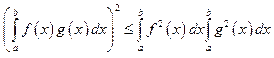 ;
;
4)
Неравенство Геллера.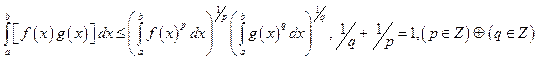 ;
;
5)
Неравенство Минковского.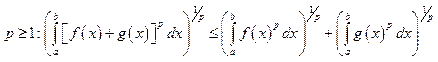 .
.
Длина кривой.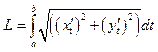 .
.
Объем тела с известным
сечением.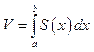 .
.
Объем тела вращения.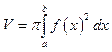 .
.
Интеграл Римана (Определенный интеграл)
Основные определения. Интегральные суммы
Определение. Пусть![]() . Разбиением
. Разбиением ![]() называется такое множество
называется такое множество![]() .
.
Определение. Любой отрезок вида ![]() называется
подотрезком разбиения.
называется
подотрезком разбиения.
Определение. ![]() - длина
- длина ![]() -ого подотрезка разбиения.
-ого подотрезка разбиения.
Определение. Мелкостью
разбиения ![]() называется
минимальная из всех длин подотрезков этого разбиения
называется
минимальная из всех длин подотрезков этого разбиения![]() . Т.к.
множество подотрезков конечно, то эта величина всегда имеет смысл, а т.к. среди
. Т.к.
множество подотрезков конечно, то эта величина всегда имеет смысл, а т.к. среди
![]() нет совпадающих, то величина всегда больше
нуля.
нет совпадающих, то величина всегда больше
нуля.
Определение.![]() .
.
Определение. Нижней
интегральной суммой Дарбу называет
выражение![]() . Верхней интегральной суммой
называют
. Верхней интегральной суммой
называют![]() .
.
Следствие.![]() .
.
Определение. На каждом ![]() выберем
выберем![]() , а совокупность всех этих точек обозначим
, а совокупность всех этих точек обозначим![]() . Назовем ее выборкой и составим интегральную
сумму Дарбу:
. Назовем ее выборкой и составим интегральную
сумму Дарбу:![]() .
.
Следствие.![]() .
.
Определение. Говорят, что разбиение ![]() вписано
в разбиение
вписано
в разбиение ![]() (
(![]() ), если
множество точек
), если
множество точек![]() , образующих
, образующих![]() , содержит в себе множество точек
, содержит в себе множество точек![]() , образующих
, образующих![]() .
.
Замечания:
3)
![]() ;
;
4)
![]() .
.
Свойства интегральных сумм
2)
Если функция ![]() ограничена на
ограничена на![]() , то при
любом выборе
, то при
любом выборе ![]() верхняя и нижняя интегральные суммы
существуют. Это следует из того, что в силу ограниченности функции ее инфимум и
супремум каждого из подотрезков будут выражаться конечными числами, а,
следовательно, все слагаемые в интегральных суммах имеют смысл.
верхняя и нижняя интегральные суммы
существуют. Это следует из того, что в силу ограниченности функции ее инфимум и
супремум каждого из подотрезков будут выражаться конечными числами, а,
следовательно, все слагаемые в интегральных суммах имеют смысл.
9)
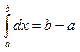 ;
;
10)
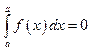 ;
;
11)
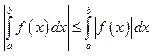 ;
;
12)
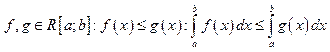 ;
;
13)
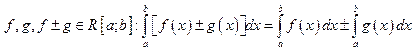 ;
;
14)
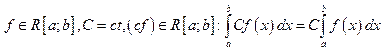 ;
;
15)
Теорема о среднем.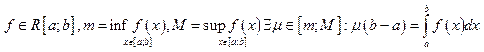 ,
где
,
где ![]() называют средним значением функции
на отрезке.
называют средним значением функции
на отрезке.
16)
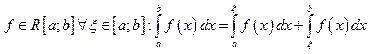 .
.
Интеграл Римана, как функция верхнего предела
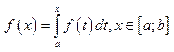
Теорема.![]() .
.
Доказательство. Пусть![]() . Чтобы показать
. Чтобы показать![]() , покажем
, покажем![]() . Для
этого
. Для
этого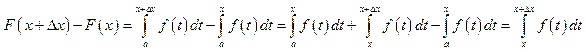 . Т.к.
. Т.к.![]() , то
, то ![]() ограничена на
ограничена на![]() .
Рассмотрим
.
Рассмотрим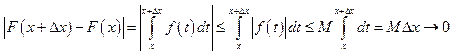 .
.
Теорема. Если![]() , то
, то ![]() является дифференцируемой в точке
является дифференцируемой в точке![]() , причем
, причем![]() .
.
Теорема. Любая непрерывная на отрезке функция ![]() имеет на этом отрезке первообразную
имеет на этом отрезке первообразную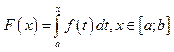 .
.
Доказательство. 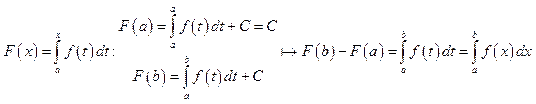 - Формула
Ньютона-Лейбница.
- Формула
Ньютона-Лейбница.
Теорема. Пусть выполняются 3 условия:
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ,
,
то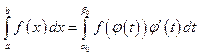 .
.
Доказательство. Поскольку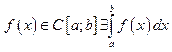 , т.к.
, т.к.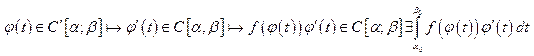 . Покажем равенство интегралов:
. Покажем равенство интегралов: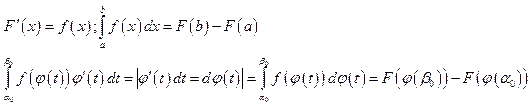 ,
,
т.к.![]() .
.
Теорема об интегрировании
по частям. Пусть функции![]() , тогда имеет место формула:
, тогда имеет место формула: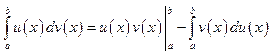 .
.
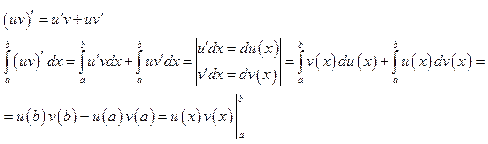 .
.
Некоторые интегральные неравенства:
6)
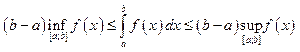 ;
;
7)
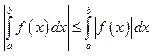 ;
;
8)
Неравенство Коши-Буняковского.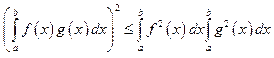 ;
;
9)
Неравенство Геллера.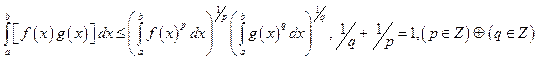 ;
;
10)
Неравенство Минковского.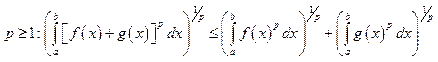 .
.
Длина кривой.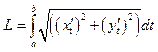 .
.
Объем тела с известным
сечением.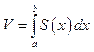 .
.
Объем тела вращения.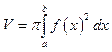 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.