Кратные несобственные интегралы Ильин т.2, с.297
1.1 Основные определения
Пусть ![]() – открытое множество
– открытое множество ![]() -мерного евклидова пространства
-мерного евклидова пространства ![]() , а
, а ![]() – его замыкание.
Последовательность
– его замыкание.
Последовательность ![]() открытых множеств монотонно
исчерпывает множество
открытых множеств монотонно
исчерпывает множество ![]() , если:
, если:
1) ![]() множество
множество ![]() содержится в
содержится в ![]() ;
;
2) объединение всех множеств ![]() совпадает
с множеством
совпадает
с множеством ![]() .
.
Пусть на открытом множестве ![]() задана
функция
задана
функция ![]() , интегрируемая
по Риману на любом замкнутом кубируемом подмножестве множества
, интегрируемая
по Риману на любом замкнутом кубируемом подмножестве множества ![]() . Будем рассматривать всевозможные
последовательности
. Будем рассматривать всевозможные
последовательности ![]() открытых множеств, монотонно
исчерпывающих
открытых множеств, монотонно
исчерпывающих ![]() и обладающих тем свойством, что
замыкание
и обладающих тем свойством, что
замыкание ![]() каждого множества
каждого множества ![]() кубируемо
(а значит, ограничено). Если для любой такой последовательности
кубируемо
(а значит, ограничено). Если для любой такой последовательности ![]() существует предел числовой
последовательности
существует предел числовой
последовательности 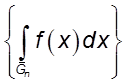 и этот предел не зависит от
выбора последовательности
и этот предел не зависит от
выбора последовательности ![]() то этот предел
называется несобственным интегралом от функции
то этот предел
называется несобственным интегралом от функции ![]() по
множеству
по
множеству ![]() и обозначается одним из следующих
символов:
и обозначается одним из следующих
символов:
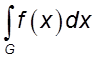 ,
, 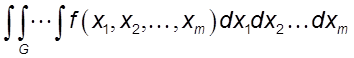 ,
,
Несобственный интеграл называется сходящимся.
Замечание: Символ используется и в случае, когда пределы указанных выше последовательностей не существуют. В этом случае интеграл называется расходящимся.
1.2 Несобственные интегралы от неотрицательных функций
Теорема 1. Для сходимости несобственного интеграла от знакопостоянной в области ![]() функции
функции ![]() ,
необходимо и достаточно, чтобы хотя бы для одной последовательности кубируемых
областей
,
необходимо и достаточно, чтобы хотя бы для одной последовательности кубируемых
областей ![]() , монотонно исчерпывающих область
, монотонно исчерпывающих область ![]() , была ограниченной числовая
последовательность
, была ограниченной числовая
последовательность 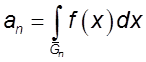 .
.
Теорема 2 (Общий признак сравнения). Пусть
неотрицательные функции ![]() и
и ![]() всюду в открытом множестве G удовлетворяют условию
всюду в открытом множестве G удовлетворяют условию ![]() . Тогда из сходимости несобственного
интеграла
. Тогда из сходимости несобственного
интеграла 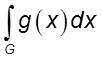 вытекает сходимость несобственного
интеграла
вытекает сходимость несобственного
интеграла 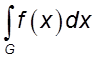 .
.
1.2 Несобственные интегралы от знакопеременных функций
Теорема. Для несобственных кратных интегралов понятия сходимости и абсолютной сходимости эквивалентны, т.е. из абсолютной сходимости следует обычная сходимость, а из обычной абсолютная.
Кратные интегралы, зависящие от параметра
1. Собственные кратные интегралы, зависящие от параметра
Пусть ![]() – произвольная точка
области
– произвольная точка
области ![]()
![]() -мерного евклидова пространства
-мерного евклидова пространства
![]() , а
, а ![]() –
точка области
–
точка области ![]() пространства
пространства ![]() . Обозначим символом
. Обозначим символом ![]() подмножество
подмножество ![]() -мерного
евклидова пространства, состоящее из всех точек
-мерного
евклидова пространства, состоящее из всех точек ![]() таких,
что точка
таких,
что точка ![]() , а точка
, а точка ![]() .
.
Пусть ![]() – функция, определенна в
– функция, определенна в
![]() , причем
, причем ![]() функция
функция
![]() интегрируема по
интегрируема по ![]() в
области
в
области ![]() . Тогда функцию
. Тогда функцию
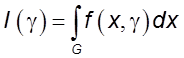 ,
,
определенную в области ![]() , называют интегралом, зависящим от
параметра
, называют интегралом, зависящим от
параметра ![]() .
.
Теорема 1 (о непрерывности интеграла по параметру). Если функция ![]() непрерывна по совокупности
аргументов в замкнутой области
непрерывна по совокупности
аргументов в замкнутой области ![]() , то интеграл – непрерывная функция параметра
, то интеграл – непрерывная функция параметра ![]() в области
в области ![]() .
.
Теорема 2 (об интегрировании интеграла по параметру). Если функция ![]() непрерывна по совокупности
аргументов в замкнутой области
непрерывна по совокупности
аргументов в замкнутой области ![]() , то интеграл можно интегрировать по параметру под знаком интеграла, т.е. справедливо равенство
, то интеграл можно интегрировать по параметру под знаком интеграла, т.е. справедливо равенство
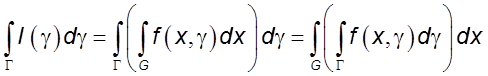 .
.
Теорема 3 (о дифференцируемости интеграла по параметру). Если функция ![]() и ее частная производная
и ее частная производная ![]() непрерывны по совокупности аргументов в
замкнутой области
непрерывны по совокупности аргументов в
замкнутой области ![]() , то интеграл имеет в области
, то интеграл имеет в области ![]() непрерывную частную производную, причем
справедливо равенство
непрерывную частную производную, причем
справедливо равенство
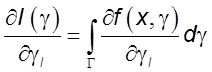 . !!!!!!! G, x
. !!!!!!! G, x
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.