

Инвариантные подпространства
Пусть ![]() .
.
Определение. Подпространство
L линейного
пространства X называется инвариантным
относительно оператора A, если ![]() .
.
Каждый линейный оператор имеет по крайней мере два тривиальных инвариантных подпространства – нулевое (только из нулевого вектора) и все пространство X. Образ и ядро линейного оператора также являются инвариантными подпространствами.
Знание
какого-либо инвариантного подпространства позволяет построить базис, в котором
матрица оператора имеет более простой вид. Действительно, пусть оператор A имеет в n-мерном
пространстве X инвариантное
подпространство L размерности m. Выберем базис ![]() в L и дополним его до базиса всего
пространства X векторами
в L и дополним его до базиса всего
пространства X векторами ![]() . Построим матицу оператора A в полученном
базисе. Поскольку
. Построим матицу оператора A в полученном
базисе. Поскольку ![]() принадлежат L, будем иметь:
принадлежат L, будем иметь:
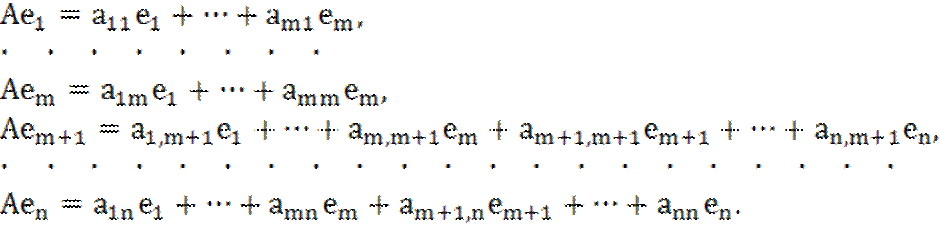 Отсюда следует, что матрица оператора A в базисе
Отсюда следует, что матрица оператора A в базисе ![]() клеточная:
клеточная:
![]()
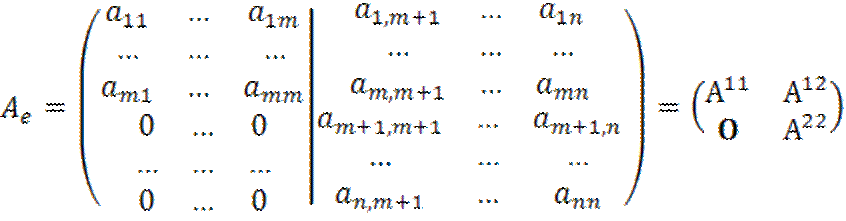 , (1)
, (1)
где ![]() - квадратная матрица порядка m,
- квадратная матрица порядка m, ![]() – квадратная матрица порядка n-m, O – нулевая
матрица размеров
– квадратная матрица порядка n-m, O – нулевая
матрица размеров ![]() ,
, ![]() - матрица размеров
- матрица размеров ![]() .
.
Предположим
теперь, что пространство X разложено в прямую сумму инвариантных
подпространств L и M. Выберем базис ![]() в X таким образом, чтобы его первые m векторов
принадлежали L, а остальные
в X таким образом, чтобы его первые m векторов
принадлежали L, а остальные ![]() векторов принадлежали M. В этом случае
образы
векторов принадлежали M. В этом случае
образы ![]() можно разложить – лишь по векторам
можно разложить – лишь по векторам ![]() , а образы
, а образы ![]() лишь по векторам
лишь по векторам ![]() . Матрица
. Матрица ![]() в соотношении (1), очевидно, будет нулевой. Поэтому
матрица
в соотношении (1), очевидно, будет нулевой. Поэтому
матрица ![]() в рассматриваемом базисе будет иметь еще более
простой вид:
в рассматриваемом базисе будет иметь еще более
простой вид:
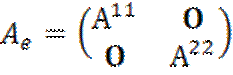 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.