Доказательства теорем: Теорема Кантора, теорема о предельной точке, об открытом множестве, об объединении и пересечении открытых и замкнутых множеств

Доказательства теорем:

1) Теорема Кантора

Формулировка: Множество действительных чисел несчетно

Доказательство: Если бы множество всех действительных чисел было счетным, то т.к. любое бесконечное подмножество счетного множества счётно, то и любое его подмножество, в частности, любой отрезок, что противоречит тому, что любой отрезок множества действительных чисел состоит из несчетного множества точек.

2) Теорема о предельной точке

Формулировка: Если (.)p – это предельная точка X, то любая окрестность (.)p содержит бесконечно много точек множества X

Доказательство: предположим, что существует такая окрестность (.)p, которая содержит конечное число точек множества X.

q_1,q_2,…,q_{n –}  это точки множества NÇX

q_i¹p, i=1,2,…,n

Рассмотрим расстояние от (.)p до всех точек q_i и выберем минимальное.

r=min r(p,q_i)>0

Построим окрестность радиуса r с центром в точке p. Nr(p)=B(p,r). Построим окрестность (.)p радиуса q. Эта окрестность не содержит ни одной точки из X.

qÎX, q¹p

По определению, (.)p не может быть предельной точкой X. Противоречие.

3) Теорема об открытом множестве

Формулировка: Множество X открыто тогда и только тогда, когда его дополнение замкнуто

Доказательство:

Необходимость:  - замкнуто

Выберем (.)xÎX. Тогда, по определению, xÏ и x не является предельной точкой множества X. Значит, существует такая окрестность N (.)x, что NÇ=, NX, а значит, x-внутренняя точка множества X. Значит, множество X – открыто.

Достаточность:  Пусть множество X – открыто и x – предельная точка , тогда каждая окрестность (.)x содержит некоторую точку из , которая не совпадает с самой точкой x. Это означает, что x не является внутренней точкой множества X и следовательно множество  замкнуто.

4) Теорема об объединении и пересечении открытых и замкнутых множеств

Формулировка:

4-1. Для любого семейства {G_a} открытых множеств G множество, которое является объединением всех G_a будет открытым

4-2. Для любого семейства {F_a} замкнутых множеств R, множество Ç всех F_a будет замкнутым

4-3. Для любого конечного семейства {G_1,G₂,…,G_n} Ç всех этих открытых множеств будет открытым

4-4. Для любого конечного семейства множеств {F_1,F_2,…,F_n} объединение всех этих множеств будет замкнутым

Доказательство:

4-1. Обозначим G=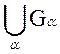 и пусть (.) xÎ G. Это означает, что xÎG_a для какого-то индекса a. Поскольку множество G_a - открытое, значит (.)x –внутренняя точка множества G_a. (.)x будет внутренней точкой множества G и значит, G – открыто.

4-2. ()=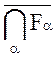

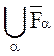
По предыдущему доказательству, множества  - открытые

Значит, 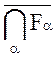 - открыто

4-3. Пусть H=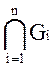. Для любой (.)x из множества H существует окрестность N_i радиуса r_i такая, что эта окрестность Î некоторому множеству G_i   xÎH      N_iG_i

Выберем из всех этих r_i минимальный min r_i=r и пусть окрестность N – окрестность (.)x радиуса r. Тогда NÎG_i. А раз NG_i, то NH

4.4. ()=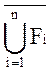

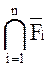
5) Принцип Архимеда

Формулировка: Каково бы ни было действительное число a, существует такое натуральное число n, что n>a

Доказательство: если бы утверждение теоремы не имело места, то нашлось бы такое число a, что для всех натуральных чисел n выполнялось бы неравенство n<=a, т.е. множество натуральных чисел N было бы ограничено сверху. Тогда, согласно тому, что всякое ограниченное сверху непустое числовое множество имеет верхнюю грань, у множества N существовала бы конечная верхняя грань:

b=sup N <+ (1)

Поскольку b-1<b, то в силу определения верхней грани найдется такое натуральное число n, что n>b-1, т.е.

n+1>b, но n+1 – также натуральное число: n+1ÎN, поэтому неравенство (n+1>b) противоречит условию (1)

6) Теорема Коши-Кантора

Формулировка: Для всякой системы вложенных отрезков существует хотя бы одно число, которое принадлежит всем отрезкам системы, причем x=sup{a_n}=inf{b_n}

Доказательство: если точки xÎ[a_n,b_n], Î[a_n,b_n], n=1,2,…,

то ясно, что для всех номеров n выполняются неравенства

|-x|<=b_n-a_n, а следовательно, в силу условия (1) для любого e>0 справедливо неравенство

|-x|<e.

Поскольку e>0 – произвольное число, то возможно только тогда, когда e=. Это означает, что существует единственное число x, принадлежащее всем отрезкам [a_n,b_n]

a_n<=x<=b_n,   n=1,2,….

Из этих неравенств видно, что число x ограничивает сверху числа a_n и снизу числа b_n, поэтому, если a=sup{a_n}, b=inf{b_n}, то в силу определения верхней и нижней граней будут выполняться неравенства

a_n<=a<=x<=b<=b_n,   n=1,2,…

Таким образом, числа a,b и x принадлежат всем отрезкам [a_n,b_n], а следовательно, они равны, и будет выполняться условие x=sup{a_n}=inf{b_n}

7) Теорема о сходящихся последовательностях

Формулировка: Пусть {p_n} – последовательность в метрическом пространстве X

7.1. {p_n} p, когда каждая окрестность (.)p содержит все члены последовательности p_n за исключением конечного числа членов последовательности

7.2. Если pÎX, p`ÎX` и последовательность p_np, p_np`, то p=p`

7.3. Если последовательность p_n сходится, то она ограничена