Расчет установившегося режима и потерь мощности, страница 5

где:

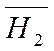 формируется так же как и Н₁ по вектору ^Т.

После (n-1) шагов будет получена верхняя треугольная форма матрицы А:

                                    Н_n-1*…*H₂*H₁*A=R                                                                                      (2.20).

Из (2.20) следует, что можно найти матрицу А:

                                    A=(H_n-1*…*H₂*H₁)^-1*R=H₁*H₂*…*H_n-1*R=H*R,         (2.21)

                                    Н=Н₁*Н₂*…*Н_n-1                                                                                                                              (2.22).

Матрица Н, как произведение ортогональных матриц, является ортогональной. Выражение (2.21) принято называть ортогонально-треугольным разложением матрицы А. Матрица Н в явном виде обычно не вычисляется, так как это требует большого объема вычислений. В действительности для восстановления матрицы Н по формуле (2.22) достаточно иметь сомножители Н_i , где i=1,2…n-1.

С другой стороны в силу специфической структуры матрицы отражения достаточно запоминать порождающие ее вектора. С учетом этих замечаний ортогонально-треугольное разложение принято размещать на месте исходной матрицы коэффициентов А. При этом в нижней части матрицы А в соответствующих столбцах хранятся вектора, порождающие матрицу отражения. Недиагональные элементы треугольной матрицы R располагаются выше главной диагонали матрицы А, а диагональные элементы R_ii, (i=1,2…n) хранятся с помощью одномерного массива RDCⁿ.

Решение системы линейных уравнений

                                    Аx=b,             AÎC^n´n,         x, bÎCⁿ

с использованием ортогонального разложения производится по следующему алгоритму:

1.  Привести матрицу коэффициентов к верхней треугольной форме (получить ортогонально-треугольное разложение) H_n-1*…*H₂*H₁*A=R;

2.  Вычислить Y=H_n-1*…*H₂*H₁*b;

3.  Решить обратной подстановкой систему линейных уравнений Rx=Y

Ортогонально-треугольное разложение особо эффективно в  случае многократного решения системы линейных уравнений с разными правыми частями:

                              Ax=b^s, s=1,…m                                                                                   (2.23).

Алгоритм решения будет следующим:

1.  Получить ортогонально-треугольное разложение;

2.  Положить s=1;

3.  Вычислить Y=H_n-1*…*H₂*H₁*b^s;

4.  Решить обратной подстановкой систему линейных уравнений Rx=Y;

5.  Присвоить s=s+1;

6.  Если s≤m, то выполнить пункт 3;

7.  Завершить счет.

2.3.5.  Организация проверки окончания счета

Проверка окончания счета может быть реализована с помощью следующей блок схемы:

ZAV – вспомогательная переменная логического типа,

e - заданная точность расчетов;

1 – переход к пункту 6 в алгоритме расчета режима методом поочередного

вычисления векторов тока и напряжения (параграф 2.3.1.). Блок-схема приведена на рисунке 2.2.

 

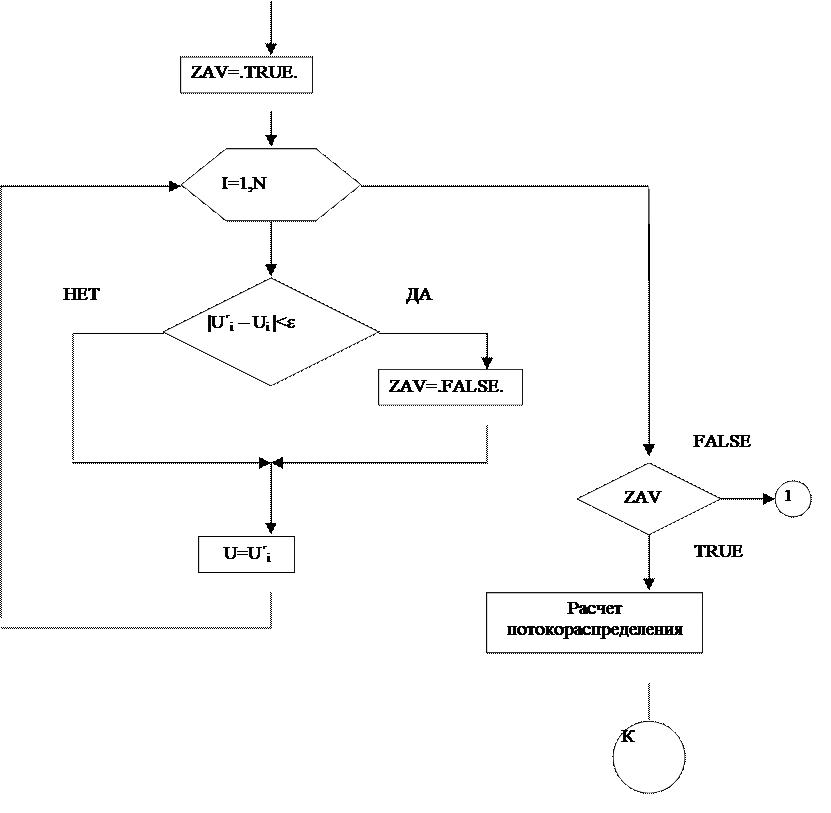Рис.2.2. Блок-схема проверки окончания счета.

2.3.6.  Расчет потокораспределения

После вычисления напряжений в узлах проводится расчет потокораспределения в декартовых координатах по следующим формулам [1]:

Для узла:

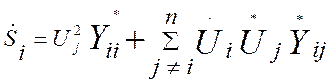                                           (2.24)

Для ветви:

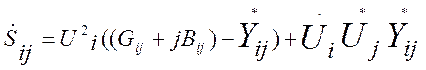                              (2.25)

Для начала трансформаторной ветви:

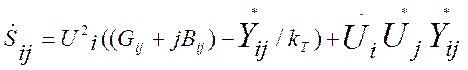                            (2.26)

Для конца трансформаторной ветви:

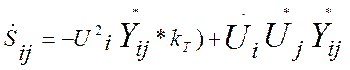                                         (2.27)

где:

– мощность в i – узле;

–поток мощности по ветви (i, j).

Расчет потокораспределения реализуется по блок-схеме, представленной на рис.2.3:

SV – значение потока мощности в ветви;

VI – значение тока в ветви;

SU – значение мощности в узле;

2.4. Расчет и анализ потерь мощности

Потери мощности  в элементах сети можно разделить на три вида:

§  нагрузочные потери,

§  потери холостого хода,