Расчет установившегося режима и потерь мощности, страница 2

§  для схемы замещения реальных электрических систем диагональные элементы матрицы  отличны от нуля и, как правило, по модулю превосходят недиагональные элементы соответствующей строки или столбца;

§  количество отличных от нуля недиагональных элементов матрицы равно удвоенному числу ветвей схемы замещения. Для больших систем, где значение n+1 велико количество ненулевых элементов будет составлять незначительную часть общего числа элементов матрицы. Матрицы, обладающие такими свойствами, называются разреженными или слабо заполненными.

Учет указанных свойств позволяет существенно повысить вычислительную эффективность алгоритмов и программ расчета установившихся режимов электрических систем на ЭВМ и во многом определяет выбор современных методов расчета.

Еще одно свойство матрицы  состоит в том, что эта матрица является особенной. Ранг матрицы  размерностью n+1 будет равен n, что позволяет задать балансирующий узел.

После выделения балансирующего узла (2.2) перепишется в виде:

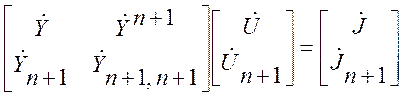.                           (2.3)

Для n независимых узлов получаем новую систему уравнений.

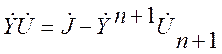,                                                          (2.4)

,                                                                        (2.5)

где:

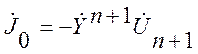,                                                                                           (2.6)

 - квадратная матрица порядка n, полученная из исходной матрицы  вычеркиванием строки и столбца, соответствующего балансирующему узлу;

 - n+1 столбец из n элементов матрицы  (кроме диагонального);

или по другому:

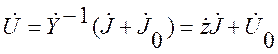,                                                  (2.7)

где:

,

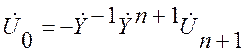.                                                                                      (2.8)

Уравнения (2.4), (2.5), (2.7) линейны и поэтому всегда имеют единственное решение. В реальных энергосистемах заданными являются не задающие токи, а мощности в узлах. Поэтому вместо (2.5), (2.7) приходится использовать уравнения вида:

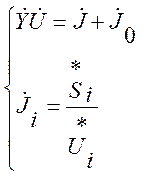, i=1,2. . .n                                                     (2.9)

где:

   - задающие токи.

Объединив эти уравнения получим:

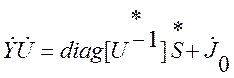                                                                                                                     (2.10).

Для (2.7) аналогично:

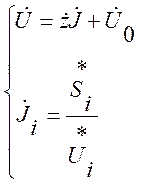                                    , i=1,2. . . n                                                                           (2.11),

или объединив оба уравнения:

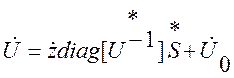                                                                                                                    (2.12).

Выражения (2.10) и (2.12) называются соответственно прямой и обращенной формой уравнений установившегося режима.

В отличие от уравнений (2.5) и (2.7), которые являются линейными и имеют единственное решение, уравнения (2.10) и (2.12) нелинейные и могут иметь:

§  единственное решение,

§  множество решений,

§  ни одного решения.

В полярной системе координат уравнения установившегося режима запишутся в виде:

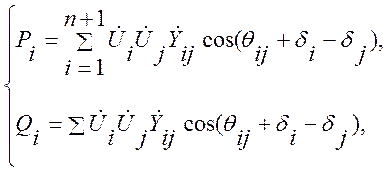                                                                                              (2.13)

где:

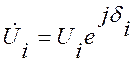  -  напряжение i-го узла,

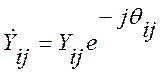  -  элемент матрицы узловых проводимостей.

2.3. Метод поочередного вычисления векторов

напряжений и токов

2.3.1. Основные положения

При расчете установившегося режима методом поочередного вычисления векторов напряжений и токов используется обращенная форма записи уравнений [1]:

                                   

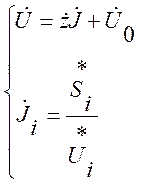
 Для организации вычислительного процесса необходимо задать начальные приближения (_i=_{i ном}, i=1,2…n) и вычислить

                              

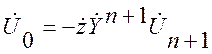
Вычисления могут быть реализованы по следующему алгоритму:

1.  Задать начальные приближения (_i=_{i ном}, i=1,2…n+1);

2.  Рассчитать ;

3.  Вычислить задающие токи: 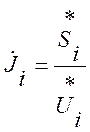,      i=1,2…,n;

4.  Вычислить новые значения узловых напряжений: ;