Электротехника \ Электроснабжение промышленных предприятий

Расчет установившегося режима и потерь мощности, страница 3

5.  Если    (где e>0 - точность расчета), то  и выполнить пункт 3;

6.  Завершить счет.

В современных программах: в явном виде не вычисляется, а обычно используется одна из неявных форм обратной матрицы. С учетом этого алгоритм расчета режима, использующий ортогонально- треугольное разложение матрицы узловых проводимостей будет следующим:

1.  Ввести исходные данные;

2.  Сформировать матрицу узловых проводимостей;

3.  Получить ортогонально-треугольное разложение матрицы узловых проводимостей: ;

4.  Задать начальное приближение: i=i ном; i=1,2,….,n+1;           Вычислить ;

5.  Положить k=0;

6.  Присвоить k=k+1;

7.  Если k>kmax (kmax – максимально допустимое число итераций), то завершить счет;

8.  Вычислить задающие токи 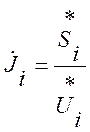, i=1,2,….,n;

9.  Преобразовать правую часть системы уравнений: ;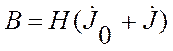

10.  Решить обратной подстановкой R=B;

11.  Если не выполняется условие 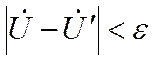, то  и выполнить пункт 6;

12.  Рассчитать потокораспределение;

13.  Завершить счет.

Пункты данного  алгоритма детализируются по мере необходимости.. Рассмотрим каждый пункт отдельно более подробно.

2.3.2. Подготовка исходных данных

Исходные данные включают в себя параметры узлов и параметры ветвей.

Под параметры каждого узла отводится запись вида:

NU       KOD        UNOM          PN      QN           PG            QG,

где:

NU – номер узла;

KOD – код узла, который принимает следующие значения:

§  3 – в качестве независимых параметров режима задаются (P, Q);

§  2 – (d, Q);

§  1 – (U, P);

§  0 -  независимые параметры режима не задаются.

UNOM –задаваемое (KOD=1) или номинальное напряжение (кВ);

PN – значение активной мощности нагрузки в узле (МВт);

QN – значение реактивной мощности в узле (МВар);

PG - значение активной генерируемой мощности в узле (МВт);

QG – значение реактивной генерируемой мощности в узле (МВар).

Параметры ветвей задаются записью:

NA       KO           R        X         G       B         TK            TK1,

где:

NA – номер узла начала ветви;

KO – номер узла конца ветви;

Для обычной ветви (ЛЭП) выбор начала и конца ветви произвольный, для шунта значение КО=0, для трансформаторной ветви началом ветви всегда является узел низшего напряжения;

R – значение активного сопротивления ветви (Ом);

X – значение реактивного сопротивления ветви (Ом);

G – активные поперечные проводимости ветви, для ЛЭП на всю длину (106/Ом);

B – реактивные поперечные проводимости ветви, для ЛЭП на всю длину (106/Ом),

§  В<0 – проводимости емкостного характера (ЛЭП),

§  B>0 – проводимости индуктивного характера (трансформаторная ветвь);

TK – значение модуля коэффициента трансформации, kT=UH/UB£1;

TK1 – значение угла коэффициента трансформации.

2.3.3. Формирование матрицы узловых проводимостей

Формирование матрицы узловых проводимостей осуществляется по следующим правилам:

§  каждый диагональный элемент матрицы Yii(i=1,2. . . n+1) равен сумме проводимостей ветвей, связанных с узлом i;

§ каждый недиагональный элемент матрицы Yi j(i, j,=1,2. . . n+1, i¹j) равен взятой с обратным знаком сумме проводимостей ветвей, связывающих узлы i и j.

Очевидно, что изменение параметра ветви i и j влияет только на 4 элемента матрицы узловых проводимостей: Yi i, Yj j, Yj i и Yi j. Следовательно, для вычисления матрицы узловых проводимостей достаточно для каждой ветви уточнить 4 элемента: Yi i, Yj j, Yj i иYi j. Этот процесс повторяется для всех L ветвей.

Для электрических сетей, содержащих трансформаторные ветви, ряд параметров требуется приводить к соответствующей ступени напряжения. Объем вычислений существенно сокращается, если данное обстоятельство учитывается при формировании матрицы узловых проводимостей.

Пусть в качестве примера рассматривается фрагмент электрической сети, приведенный на рисунке 2.1.

Скачать файл