Расчет установившегося режима и потерь мощности, страница 4

 

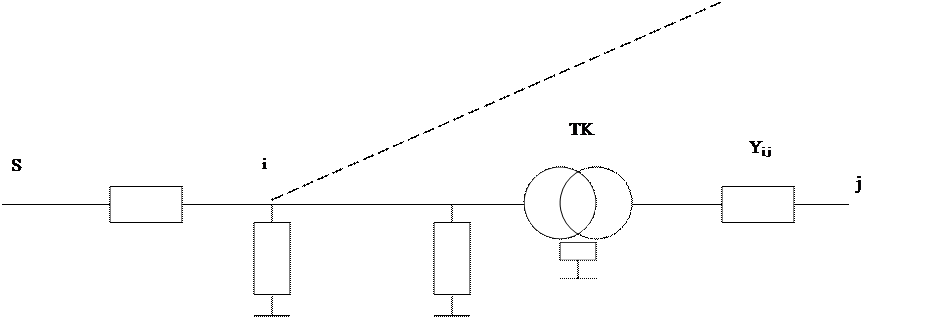
Рис. 2.1. Часть электрической сети, содержащей трансформаторную ветвь.

Уравнения потокораспределения для к-ой ветви:

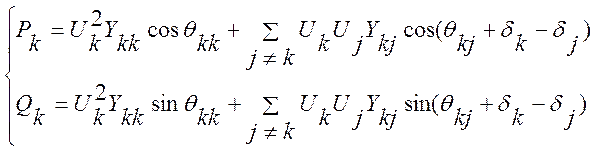                                                     (2.14)

Анализ выражения (2.14) показывает, что:

1.  Если k=i (начало трансформаторной ветви), то смешанные произведения _kjY_{j k} будут содержать проводимость трансформаторной ветви, приведенную к высшему напряжению. Это означает, что _i также должно приводиться к высшему напряжению. Для этого достаточно при формировании матрицы узловых проводимостей учесть, что _{i j}@-_{i j}/_{T i j}.  Слагаемое  вида _i²_ij  будет содержать  составляющую  _{ii j}, в которой напряжение _i также необходимо привести к высшему напряжению. Этого можно добиться, если при формировании матрицы узловых проводимостей _{i i}  вычислять по формуле: _{i i}@_{i j}/k_{T i j} (_{i j} – проводимость ветви (i, j)).

2.  Если k=j (конец трансформаторной ветви), то смешанное произведение _{iji j} cодержит составляющие вида _ij(-_{i j}) (_{i j} – приведено к высшему напряжению), и _i также необходимо привести к высшему напряжению. Этого можно добиться, если при формировании матрицы узловых проводимостей,        _{i j}=_{j i}= - _{i j}/_{T i j}.

С учетом этих замечаний алгоритм формирования матрицы узловых проводимостей будет следующим:

1.  Задать начальные приближения: Y=0+j0;

2.  Положить К=1;

3.  Зафиксировать начало и конец K-ой ветви, то есть I=NA(K), J=KO(K);

4.  Определить проводимость на землю: Y0=G(K)-jB(K);

5.  Если шунт (J=0), то выполнить пункт 9;

6.  Вычислить Y1=1./(R(K)+jX(K));

7.  Если ветвь трансформаторная,  то:

                Y(J,J)=Y(J,J)+Y1

                Y1=Y1/TK

                 Y0=Y0+Y1/TK

иначе:

                 Y0=Y0+Y1

                 Y(J,J)=Y(J,J)+Y0

8.  Вычислить: Y_{i j}=Y_{i j}-Y1, Y_{j i}=Y_{j i}-Y1;

9.  Вычислить проводимость i-го узла: Y_{i i}=Y_{i i}+Y0;

10.  Присвоить K=K+1

11.  Если K≤L, то выполнить пункт 8 (L – количество ветвей);

12.  Завершить счет.

Где параметры  I, J, K, L, NA, KO  –  целого типа, а Y, Y1,Y0  -  комплексного, (Y -  матрица узловых проводимостей, Y1, Y0 – вспомогательные переменные).

2.3.4. Ортогонально-треугольное разложение матрицы

С помощью матриц отражения матрицу  общего вида можно привести к верхней треугольной форме. Для этого достаточно выполнить (n-1) шаговый процесс. На первом шаге необходимо в первом столбце матрицы А аннулировать все элементы, начиная со второго. Для этого достаточно рассмотреть ортогональную (Н^T=Н^-1=H)матрицу отражения:

                                     Н₁=[I-2b²*J*J^т),                                                                                           (2.14)

где:

                               J=[а₁₁±s₁, a₂₁. . .,a_n1]^Т,

a₁₁, a₂₁, . . .a_n1 – элементы первого столбца матрицы А,

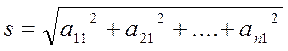                               ,                                                                                   (2.15)

                               2b²=1/ã₁₁J₁    ,                                                                                                                                               (2.16)

                               ã₁₁=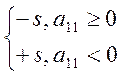                                                                                                     (2.17)

В результате умножения слева А на матрицу отражения получим:

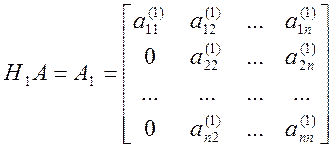                                                                                                      (2.18).

На втором шаге надо использовать такую матрицу отражения, которая с одной стороны, оставляет неизменным первый столбец матрицы А₁, с другой стороны, обнуляет во втором столбце все элементы, начиная с третьего. Этого можно добиться, если матрицу отражения Н₂ составить так:

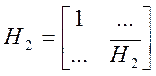                                                                                                                               (2.19).