2. РАСЧЕТ УСТАНОВИВШЕГОСЯ РЕЖИМА И
ПОТЕРЬ МОЩНОСТИ
2.1. Постановка задачи
При использовании любой из методик для расчета потерь электроэнергии необходима информация, которая может быть получена при расчете установившегося режима:
§ потоки активной и реактивной мощности в каждой из ветвей;
§ значения потерь активной и реактивной мощности в каждой из ветвей;
§ значение напряжения в узлах;
§ потери активной и реактивной мощности в ветвях схемы.
В соответствии с заданием на дипломный проект расчет установившегося режима должен проводиться методом поочередного вычисления векторов напряжения и токов.
Путь рассматривается электрическая система, содержащая n+1 узел. Узлы, на которые работает электростанция, а также источники реактивной мощности (синхронные компенсаторы, батареи статических конденсаторов, источники реактивной мощности), называются генераторными. Остальные узлы – называются нагрузочными узлами.
Активные и реактивные сопротивления ветвей, их поперечные проводимости ветвей, а так же коэффициенты трансформации трансформаторов – называются параметрами системы. Предполагается, что все параметры системы известны. Исключением могут быть коэффициенты трансформации, допускающие регулирование, которые должны быть получены в результате расчета режима.
Режим электрической системы характеризуется такими параметрами как: генерируемые мощности генераторных узлов, активные и реактивные мощности нагрузок, токи, соответствующие нагрузкам (токи в узлах), потоки мощности, а так же токи в ветвях, модули и фазы узловых напряжений либо их действительные и мнимые части (в зависимости от выбранной для расчета системы координат). Система координат выбирается в зависимости от представления исходных данных и вида, в котором будут использоваться результаты расчета.
Состояние линейной электрической цепи описывается уравнениями, составленными на основе первого и второго законов Кирхгофа и закона Ома. В расчетной практике широкое применение получили преобразованные - контурные и узловые – уравнения. Относительная сложность формирования контурных уравнений для разветвленных электрических цепей с большим числом элементов, существенная зависимость свойств этих уравнений от выбранной системы контуров, а также увеличение количества ветвей схемы замещения электрической системы при задании активных элементов источниками ЭДС – все это привело к тому, что в расчетах установившихся режимов электрических систем на ЭВМ контурные уравнения используются гораздо реже, чем узловые.
Для системы с n+1 узлами можно составить n+1 узловых уравнений. Исключая уравнение, соответствующее так называемому “балансирующему” узлу и задавая в одном из узлов, называемого “базисным”, значения напряжения получим систему из n линейно независимых узловых уравнений.
Балансирующий узел совмещают с базисным и присваивают ему наибольший номер n+1, а в качестве независимых параметров режима в этом узле задают модуль и угол напряжения: Un+1, dn+1 для полярной системы координат или действительная и мнимая часть напряжения U’ и U” для декартовой системы координат. В дальнейшем этот узел будем называть балансирующим.
В остальных n узлах необходимо задать по два
независимых параметра режима. В нагрузочных узлах в качестве независимых
параметров режима задается ![]() iи
iи ![]() ,
которые берутся либо по результатам предыдущего расчета, либо по аналогии с
имевшими место измерениями. В генераторных узлах в качестве независимых
параметров режима могут задаваться:
,
которые берутся либо по результатам предыдущего расчета, либо по аналогии с
имевшими место измерениями. В генераторных узлах в качестве независимых
параметров режима могут задаваться:
§
(![]()
![]() ),
),
§
(![]()
![]() ).
).
Активные мощности в генераторных узлах определяется либо по результатам оптимизации режима по активной мощности, либо по результатам эксплуатационных и контрольных замеров. Модуль напряжения и реактивная мощность определяется по результатам эксплуатационных и контрольных замеров либо по имевшим место аналогичным измерениям.
При известных параметрах электрической системы и независимых параметрах режима расчет сводится к решению системы нелинейных уравнений вида:
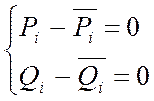 , где: i=1,2,3 . . . n (2.1)
, где: i=1,2,3 . . . n (2.1)
В дальнейшем
предполагается, что во всех узлах в качестве задаваемых параметров режима
используются ![]() и
и ![]() . В
выражении (2.1)
. В
выражении (2.1) ![]() ,
, ![]() , i=1,2. . . n – Заданные независимые параметры режима, а Pi и Qi - их расчетные значения (Pi(U,d), Qi(U,d).
, i=1,2. . . n – Заданные независимые параметры режима, а Pi и Qi - их расчетные значения (Pi(U,d), Qi(U,d).
В балансирующем узле Pn+1 и Qn+1 должны быть получены в результате расчета режима с учетом потерь мощности в электрической сети. Это означает, что в качестве балансирующего узла необходимо выбирать одну из наиболее мощных электростанций. Таким образом, расчет установившегося режима сводится к решению системы (2.1) при заданных параметрах системы и независимых параметрах режима, то есть к нахождению действительной U’ и мнимой U” части напряжения, зная которые можно легко рассчитать остальные параметры режима.
2.2. Форма записи уравнений установившегося режима
По методу узловых потенциалов [1]:
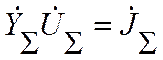 ,
, ![]() ÎС(n+1)´(n+1),
ÎС(n+1)´(n+1), ![]() ÎС(n+1); (2.2)
ÎС(n+1); (2.2)
где:
![]() -
квадратная матрица узловых проводимостей порядка n+1. Формирование матрицы
-
квадратная матрица узловых проводимостей порядка n+1. Формирование матрицы ![]() описано
ниже в пункте 2.3.4.
описано
ниже в пункте 2.3.4.
Свойства матрицы ![]() следующие:
следующие:
§ матрица ![]() симметрична;
симметрична;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.