Зонная теория металлов, диэлектриков и полупроводников, страница 4

При контакте металла с собственным п/п искривление энергетических зон сопровождается увеличением проводимости в приповерхностном слое.

Глубина проникновения поля

,

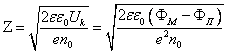Поскольку .

Таким образом, чем меньше степень легирования n₀ и чем больше разность работ выхода электронов из металла и полупроводника, тем больше глубина проникновения в п/п электрического поля, вызванного контактной разностью потенциалов.

Контакт электронного и дырочного полупроводников (р-n переход).

Это нами изучено на стр.12-20.

Равновесное состояние.

При термодинамическом равновесии, при котором состояние электрона описывается равновесной функцией распределения

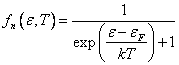           (статистика Ферми-Дирака)

движение электрона в кристалле обуславливается  тепловой энергией. Поэтому для равновесного случая можно записать

,                                            (1)

где  - объем зоны Бриллюэна;

 – вероятность перейти электрону за 1сек. Из состояния  в состояние ;  – волновые векторы электрона;

 - функции распределения в соответствующих состояниях;

 - время жизни в состоянии .

Из этого соотношения следует, что в системе, находящейся в равновесном состоянии, имеет место равенство потоков электронов для прямого и обратного процессов, что согласуется с принципом детального равновесия.

На основании (1) нетрудно получить

                                                                (2)

Подставляя в уравнение (2) выражение для равновесной функции  будем иметь

                                                              (3)

где  - полная энергия и уровни Ферми для электронов с волновыми векторами  и  соответственно.

Так как в условиях термодинамического равновесия полная энергия электронов  не меняется, то , откуда следует, что

.

Таким образом, в равновесном состоянии во всех частях системы между которыми может происходить переход электронов, положение уровня Ферми одинаково.

Лекция 11.

Поверхностные явления в полупроводниках.

Для бесконечного кристалла в случае сильно связанных электронов, как следует из решения уравнения Шредингера, достаточно рассматривать две зоны разрешенных значений энергии – зону проводимости и валентную зону. В ограниченном же кристалле, кроме зон разрешенных энергий, на его поверхности вследствие разрыва периодичности кристаллической решетки  возникают поверхностные состояния, энергетические уровни которых расположены в запрещенной зоне. Эти уровни теоретически были предсказаны Таммом и носят название уровней Тамма. Поверхностная концентрация таммовских уровней определяется концентрацией поверхностных атомов и составляет величину .