Министерство образования Российской Федерации
ХАБАРОВСКИЙ
ГОСУДАРСТВЕННЫЙ
ЛАБОРАТОРНЫЙ
ПО ЭКСПЕРИМЕНТАЛЬНОЙ
ФИЗИКЕ
 |
|||
 |
|||
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
 |
«ИЗМЕРЕНИЕ ИНДУКТИВНОСТЕЙ И
ЁМКОСТЕЙ МЕТОДОМ АМПЕРМЕТРА И
ВОЛЬТМЕТРА. ПРОВЕРКА ЗАКОНА ОМА
ДЛЯ ПЕРЕМЕННОГО ТОКА»
 |
Хабаровск 2000
§ 1. Понятиео
квазистационарном токе
При действии в замкнутой цепи переменной э.д.с. в ней воз-никает пееменный ток. Конечная скорость распространения элек-тромагнитного поля приводит к тому, что сила тока в различных сечениях неразветвлённого проводника оказывается не одинако-вой в один и тот же момент времени. Однако, если сила тока мало меняется за время t , в течение которого электромагнитное возму-щение пробегает расстояние до самых удалённых частей цепи, то мгновенные значения силы тока во всех сечениях неразветвлё-нной цепи можно считать практически одинаковыми. Токи, подчиняющиеся такому условию, называются квазистацио-нарными.
Для периодически изменяющихся гармонических токов усло-вие квазистационарности записывают следующим образом
 |
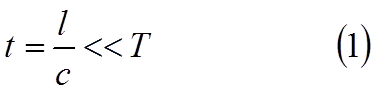где l – расстояние до самой удалённой части цепи;
с – скорость распространения электромагнитных возмущений (скорость света);
Т – период изменения переменной э.д.с.
Так, например, ток промышленной частоты ( f = 50 Гц , Т = 0,02 с ) можно считать квазистационарным для цепей длиной до 100 км . При размерах цепи порядка 3 м квазистационарными могут считаться токи частотой до 106 Гц .
Мгновенные значения квазистационарных токов подчиняют-ся закону Ома, следовательно, для них справедливы правила Кирхгофа.
§ 2. Активное сопротивление
в цепи переменного тока
Активным (или омическим) называется такое сопротивле-ние R , которое не обладает индуктивностью и ёмкостью. Поня-тие «чисто активного» сопротивления (как и «чисто ёмкостного» и «чисто индуктивного») является абстракцией, так как всякий проводник (например, прямолинейный отрезок провода) обладает некоторой индуктивностью и ёмкостью.
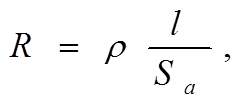Активное сопротивление
есть не что иное, как сопротивление проводника (или участка цепи) постоянному
току
где Sa – сечение той части проводника, по которой «течёт» пере-менный ток (см. скин-эффект).
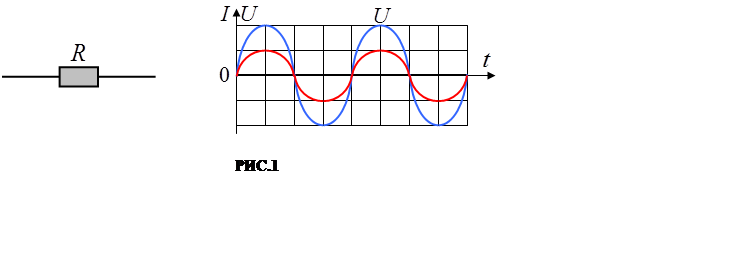
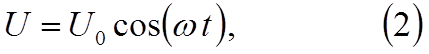Пусть к зажимам такого
активного сопротивления (РИС.1) приложено напряжение, изменяющееся по закону
где Uo– амплитудное значение напряжения;
ω = 2π f – круговая частота;
t – время.
 |
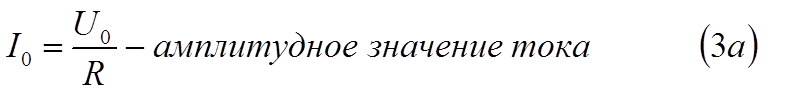
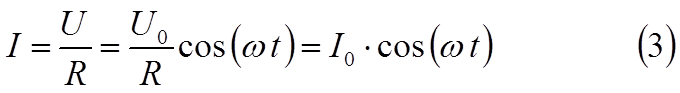Если выполняется условие квазистационарности, то ток через
сопротивление R определяется законом Ома
 |
где
На РИС.1 графически представлено изменение со временем напряжения и силы тока (осциллограммы) для частного случая R = 2 Ома .
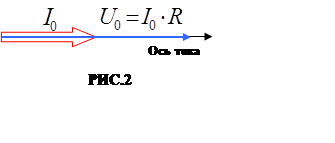Соотношение
между переменными токами и напряжениями можно сделать особенно наглядными, если
их изображать с по-мощью векторов. Для этого выберем произвольное направление,
которое назовём осью тока, отложим вдоль этого направления вектор
тока длиной lo (РИС.2). Пос-кольку напряжение (2) и ток (3)
изме-няются синфазно (совпадают по фазе), вектор напряжения Uo = Io R также
будет направлен вдоль оси тока.
Совокупность векторов напряжений и токов образует векторную диаграмму данной цепи.
§ 3. Индуктивность в
цепи переменного тока
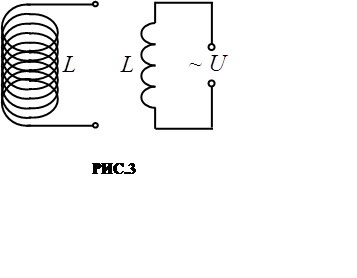
Переменное напряжение (2) подадим на зажимы катушки, об-ладающей пренебрежимо малым активным и ёмкостным сопро-тивлением. По катушке (РИС.3) начнёт течь переменный ток. В результате явления самоиндукции, в ней во-зникнет э.д.с. индукции, которая, в соответст-вии с правилом Ленца, всегда направлена так, что препятствует изменениям тока, текущего в цепи.
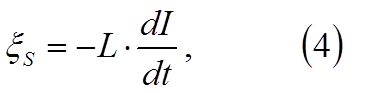
Если
катушка не содержит ферро-магнетиков, то выражение для э.д.с. индукции имеет
вид
где L – коэффициент пропорцио-нальности между током Iи создава-емым им полным магнитным потоком через катушку (сцеплённым потоком) Ψ = L I . Коэффициент пропроциональности Lназывается индуктив-ностью катушки (контура, проводника).
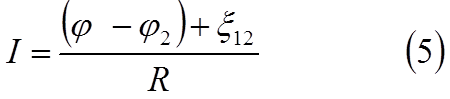В соответствии с
законом Ома для неоднородного участка цепи, ток в нём
Положив в (5) R = 0 , φ1 – φ2 = U~ и ξ12 = ξs ,можем написать для схемы, изображённой на РИС.3
 |
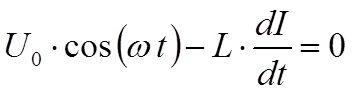Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
