Решение такого квадратного уравнения не составляет особо-го труда, однако, мы намерены продемонстрировать вам вектор-ный способ решения такого уравнения, как наиболее простой и наглядный. Для этого нам потребуются лишь сведения получен-ные выше.
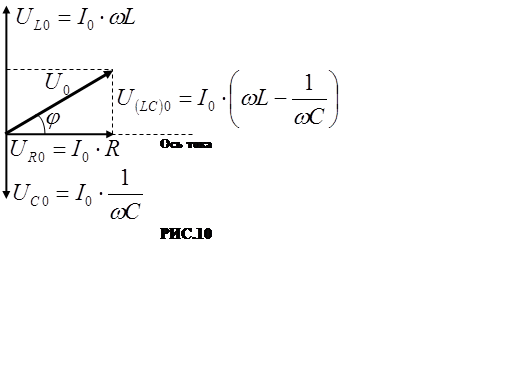Построим
векторную диаграмму нашей цепи, для чего выбе-рем некоторое направление оси
тока (РИС.10). Поскольку ток квазистационарный, то в каждый данный момент
времени на всех участках последователь-ной цепи (РИС.9) ток одинаков.
Угол φ даёт разность фаз между напряжением U и силой тока I. Из прямоу-гольного треугольника, гипотенуза которого Uo cледует, что :
 |
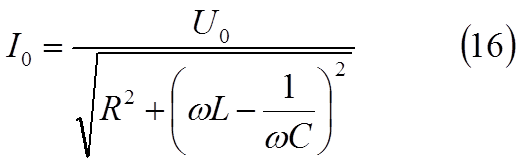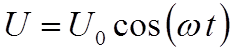Итак, если
напряжение на зажимах полной цепи изменяется по закону
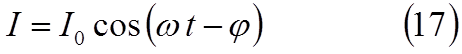то в цепи течёт ток
где Io определяется формулой (16), а φ определяется из условия
 |
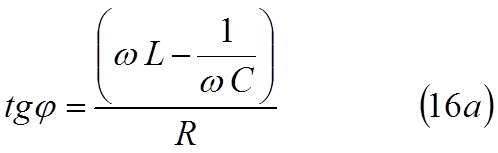Величина
 |
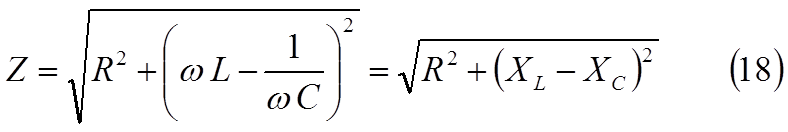называется полным сопротивлением цепи, а отношение (16) – законом Ома для полной цепи переменного тока. Величина
 |
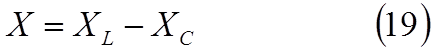называется реактивным сопротивлением.
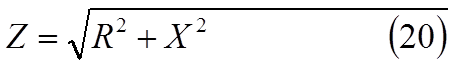Таким образом
В соответствии с (16а) ток отстаёт от напряжения (φ > 0) или опережает его (φ < 0) в зависимости от соотношения между XL и XC . При XL > XC ток отстаёт от напряжения, при XL < XC ток опережает напряжение. Если XL = XC изменения тока и напряжения происходят синфазно.
 |
Лабораторная
работа №11
«ИЗМЕРЕНИЕ ЁМКОСТЕЙ И
ИНДУКТИВНОСТЕЙ МЕТОДОМ
АМПЕРМЕТРА И ВОЛЬТМЕТРА.
ПРОВЕРКА ЗАКОНА ОМА ДЛЯ
ПЕРЕМЕННОГО ТОКА»
ЦЕЛЬ РАБОТЫ: «Научиться измерять ёмкость и индук-тивность методом амперметра и вольтметра. Проверить за-кон Ома для полной цепи переменного тока.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: 1) источник переменного на-пряжения с регулируемым выходом (В-24); 2) индуктивность до 1 Гн с известным активным сопротивлением; 3) магазин ёмкостей; 4) мно-гопредельные амерметр и вольтметр; 5) соединительные провода.
УПРАЖНЕНИЕ 1. Определение активных сопротивлений используемых приборов. (Выполняется при самоподготовке).
1. Воспользовавшись экспериментальными результатами лабо-раторной работы №4, восстановите величину омического (ак-тивного сопротивления катушки индуктивности.
2. По паспортным данным установите активные сопротивления используемых амперметра и вольтметра на всех пределах изме-рений.
УПРАЖНЕНИЕ 2. Измерение коэффициента самоиндук-ции катушки и ёмкости конденсаторов.
ЗАДАНИЕ 1: измерение коэффициента самоиндукции катушки.
1.
 |
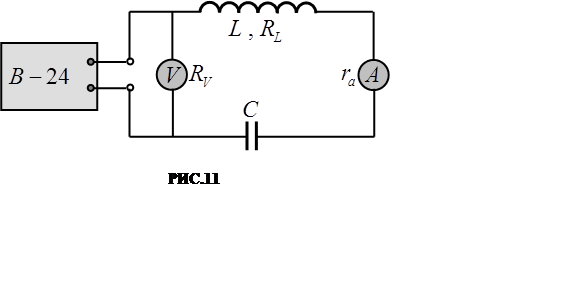2. С помощью проводника закоротите магазин ёмкостей С.
3. Включите источник переменного тока и, плавно вращая регулятор напряжения по часовой стрелке, установите ток и напряжение в це-пи, при которых обеспечивается наилучшее качество измерений (при измерениях, во избежание сильного нагревания катушки из-за большого её активного сопротивления, не пропускайте длительно ток более 0,25 А).
4.
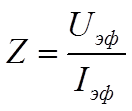По
формуле
вычислите полное сопротивление катушки.
5.
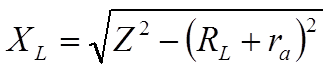Зная
(из предыдущего упражнения) величины активных сопротив-лений, вычислите
величину индуктивного сопротивления катушки по формуле
6.
Используя соотношение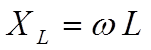 
, найдите величину коэффици-ента
самоиндукции катушки L.
7. Оцените в % точность определения величин XL и L.
ЗАДАНИЕ 2: определение ёмкости конденсаторов магазина ёмко-стей.
1. С помощью проводника-короткозамыкателя отключите катушку и включите магазин ёмкостей.
2. Подключите в схему один из конденсаторов из магазина ёмкостей и действуя аналогично заданию 1, измерьте значения Uэф и Iэф и вы-числите полное сопротивление электрической цепи в этом случае.
3. По соответствующим формулам вичислите ёмкостное сопротивле-ние ХС и ёмкость С данного конденсатора.
4. Оцените (в %) точность измерения величин XC и С .
5.
Действуя аналогично, определите ёмкости всех номиналов
магази-на ёмкостей.
УПРАЖНЕНИЕ 3. Проверка закона Ома для полной цепи переменного тока.
1. Выберите электрическую ёмкость так, чтобы XL ≈ 2XC или XC ≈ 2XL и проверьте закон Ома для полной цепи переменного тока.
2. В выбранном масштабе постройте векторные диаграммы нап-ряжений или сопротивлений.
3. Вычислите сдвиг фазы между током в цепи и полным напряжением.
4. Результат расчёта сравните с экспериментом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.