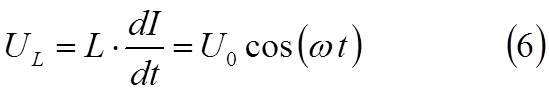 Отсюда, падение
напряжения на индуктивности
Отсюда, падение
напряжения на индуктивности
Перепишем уравнение (6) в виде
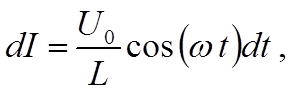 |
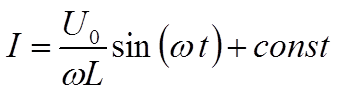 откуда, проинтегрировав, получим:
откуда, проинтегрировав, получим:
Поскольку в индуктивности действуют переменные U и ξs , то ток не может иметь постоянной составляющей, поэтому const = 0.
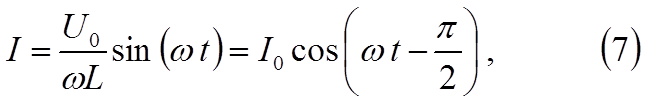
![]() Таким образом,
Таким образом,
 где
где
 Сопоставляя (3а) и (8),
видим, что роль сопротивления в дан-ном случае играет величина
Сопоставляя (3а) и (8),
видим, что роль сопротивления в дан-ном случае играет величина
которую называют реактивным индуктивным сопротивлением или просто индуктивным сопротивлением. Если взять L в генри а ω в с-1 то XL будет выражено в омах (СИ).
Как видно из (9), величина индуктивного сопротивления рас-тёт с частотой. Постоянному току (ω = 0) индуктивность сопроти-вления не оказывает.
Заменив в (6) Uo через IoωL (см. 8), получим для падения на-пряжения на индуктивности следующее выражение:
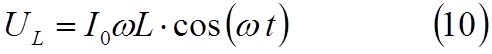 |
Сравнивая (7) и (10), видим, что падение напряжения на ин-дуктивности опережает по фазе ток, текущий через индуктив-ность на π / 2 .
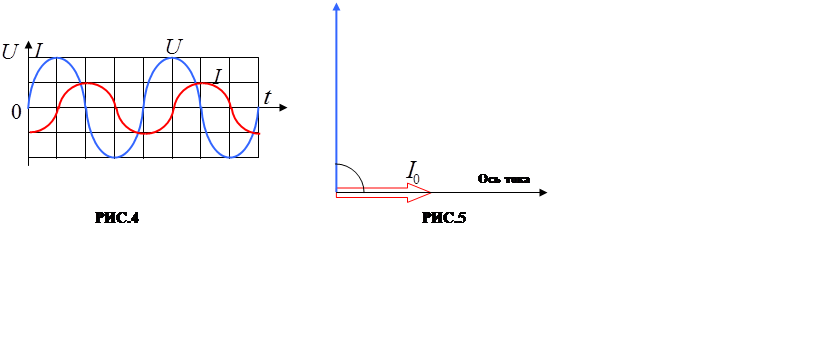
На РИС.4 колебания напряжения и тока изображены на од-ном графике. Так как в контуре с индуктивностью ток отстаёт от напряжения по фазе на угол φ = π / 2 , поэтому на осциллограмме ток достигает максимума на четверть периода позже, чем напря-жение. Если, как и на РИС.2, ось токов направить горизонтально, то вектор напряжения должен быть повёрнут относительно векто-ра тока на угол π / 2, и если за положительное направление принять вращение против часовой стрелки (как принято в эле-ктротехнике), то получается векторная диаграмма, изображённая на РИС.5.
 |
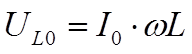 Физический смысл сдвига фаз между током и напряжением на индуктивности
можно пояснить следующим образом. Поскольку омическое падение напряжения на
индуктивности от-сутствует (R
= 0), то приложенное внешнее напряжение
источни-ка равно и противоположно направлено э.д.с. самоиндукции, но эта э.д.с.,
пропорциональная скорости изменения тока, достигает максимального значения
тогда, когда значение тока проходит че-рез нуль (см. РИС.4). Следовательно,
напряжение по фазе сдвину-то относительно тока, опережая его на 90о.
Физический смысл сдвига фаз между током и напряжением на индуктивности
можно пояснить следующим образом. Поскольку омическое падение напряжения на
индуктивности от-сутствует (R
= 0), то приложенное внешнее напряжение
источни-ка равно и противоположно направлено э.д.с. самоиндукции, но эта э.д.с.,
пропорциональная скорости изменения тока, достигает максимального значения
тогда, когда значение тока проходит че-рез нуль (см. РИС.4). Следовательно,
напряжение по фазе сдвину-то относительно тока, опережая его на 90о.
§ 4. Ёмкость в цепи
переменного тока
Подадим напряжение (2) на конденсатор ёмкостью С (РИС.6) Сопротивлением подводящих проводов и индуктивностью цепи будем пренебрегать.
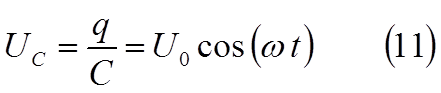
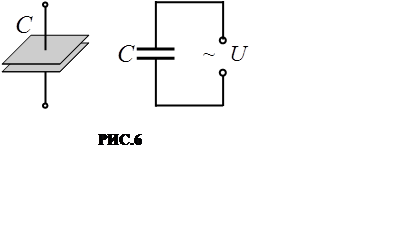 Ёмкость
непрерывно перезаря-жается, поэтому в цепи течёт пере-менный ток. Поскольку
сопротив-ление подводящих проводов пре-небрежимо мало, напряжение на
конденсаторе Uc
= q / C можно считать равным
внешнему напря-жению
Ёмкость
непрерывно перезаря-жается, поэтому в цепи течёт пере-менный ток. Поскольку
сопротив-ление подводящих проводов пре-небрежимо мало, напряжение на
конденсаторе Uc
= q / C можно считать равным
внешнему напря-жению
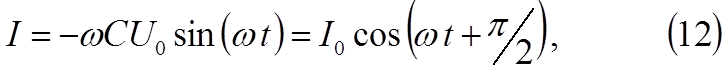 Производная
от заряда по времени даёт силу тока в цепи
Производная
от заряда по времени даёт силу тока в цепи
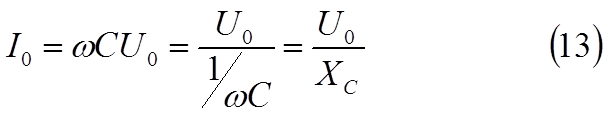 где
где
Величина Xc = 1 / ωC, имеющая размерность сопротивления, называется реактивным ёмкостным сопротивлением или прос-то ёмкостным сопротивлением.
Для постоянного тока (ω = 0) ёмкостное сопротивление Хс=∞ - постоянный ток через конденсатор течь не может. Переменный ток (ω ≠ 0) может течь через конденсатор, причём, оказываемое току сопротивление, тем меньше, чем больше частота тока и ёмкость конденсатора.
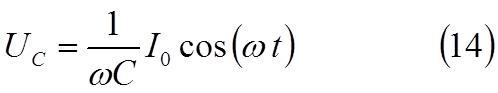 Заменив в
(11) Uo через Io∙(1
/ ωC), для падения напряжения на ёмкости
получим
Заменив в
(11) Uo через Io∙(1
/ ωC), для падения напряжения на ёмкости
получим
![]()
 Сравнивая (12) и (14), видим что падение напряжения на ём-кости отстаёт
по фазе от текущего через ёмкость тока на π /2 (РИС.7).
Причина отставания заключается в том, что до тех пор, пока течёт ток в одном и
том же направлении, заряд на конденса-торе растёт. Сила тока проходит через
максимум и начинает убывать, а заряд (а, следовательно, и Uс) всё ещё продолжает расти, достигая максимума в тот
момент, когда ток обращается в нуль. Вслед затем ток изменяет направление и
начинается уюывание зарядов (напряжения) на обкладках.
Сравнивая (12) и (14), видим что падение напряжения на ём-кости отстаёт
по фазе от текущего через ёмкость тока на π /2 (РИС.7).
Причина отставания заключается в том, что до тех пор, пока течёт ток в одном и
том же направлении, заряд на конденса-торе растёт. Сила тока проходит через
максимум и начинает убывать, а заряд (а, следовательно, и Uс) всё ещё продолжает расти, достигая максимума в тот
момент, когда ток обращается в нуль. Вслед затем ток изменяет направление и
начинается уюывание зарядов (напряжения) на обкладках.
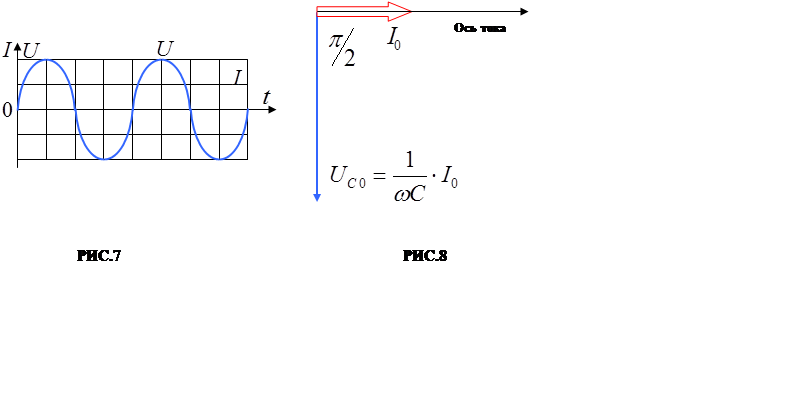 |
Векторная диаграмма цепи переменного тока, содержащей идеальную ёмкость, показана на РИС.8.
§ 5. Полная цепь
переменного тока
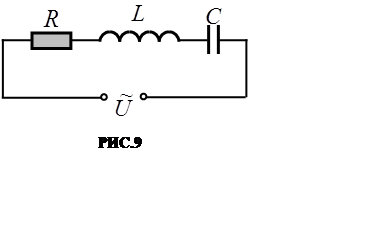
Полной цепью переменного тока называют электричес-кую цепь, состоящую из последовательно соединённых актив-ного сопротивления R, индуктивности L и ёмкости С (РИС.9).
 Подадим на концы этой цепи переменное
напряжение (2). В цепи возникнет переменный ток той же частоты ω, амплитуда Io и фаза φ ко-торого, очевидно, определяются
па-раметрами цепи R,L и C.
Подадим на концы этой цепи переменное
напряжение (2). В цепи возникнет переменный ток той же частоты ω, амплитуда Io и фаза φ ко-торого, очевидно, определяются
па-раметрами цепи R,L и C.
Как и в предыдущих случаях, считая ток квазистационарным, мо-жно составить в соответствии с правилом Кирхгофа дифференци-альное уравнение, которому должна удовлетворять сила тока в этой цепи :
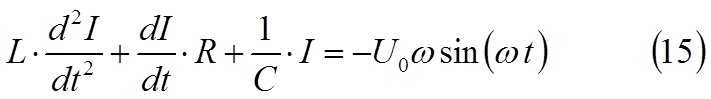 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.