Измерение сопротивлений с помощью моста Уитстона. Проверка законов соединения сопротивлений: Методическое пособие к лабораторной работе № 5

Министерство образования Российской Федерации

ХАБАРОВСКИЙ

ГОСУДАРСТВЕННЫЙ

ПЕДАГОГИЧЕСКИЙ

УНИВЕРСИТЕТ

Кафедра общей физики

Доц. В.Г.Довбило

ЛАБОРАТОРНЫЙ

ПРАКТИКУМ

ПО ЭКСПЕРИМЕНТАЛЬНОЙ

ФИЗИКЕ

 

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

 «ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ С

ПОМОЩЬЮ МОСТА УИТСТОНА.

ПРОВЕРКА ЗАКОНОВ СОЕДИНЕНИЯ

СОПРОТИВЛЕНИЙ »

Хабаровск 2000

§ 1. Электрическое сопротивление

проводников

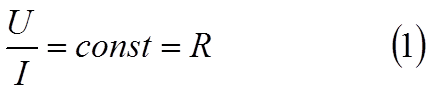На основании многочисленных опытов Ом в 1827 году уста-новил, что при постоянной температуре отношение напряжения на проводнике к току в нём является постоянной для данного проводника величиной

Величину  R , характеризующую данный проводник, Ом наз-вал сопротивлением проводника. Величина, обратная сопротив-лению проводников получила название проводимости

 Уравнение  (1)  позволяет установить единицу измерения сопротивления. Сопротивлением, равным единице, обладает про-водник, в котором при напряжении в  1 вольт возникает ток в  1 ампер. Эта единица электрического сопротивления называется омом (Ом). Единица проводимости получила название сименс. Проводимостью в 1 сименс обладает проводник сопротивлением  в 1 Ом.

Исследуя проводники различных размеров и из различных материалов, Ом нашёл, что для однородных цилиндрических и призматических проводников (проволок, лент и т.п.) сопротивление пропорционально их длине  l  и обратно пропор-   ционально площади поперечного сечения  S

  

где  ρ – коэффициент пропорциональности, называемый удель-ным сопротивлением вещества, из которого сделан проводник. Из уравнения  (3)  видно, что удельное сопротивление – это соп-ротивление куба вещества со сторонами, равными 1 метру (СИ), если ток в нём идёт параллельно одному из рёбер. Единица удельного сопротивления - Ом∙м.

Величина, обратная удельному сопротивлению, называется удельной проводимостью

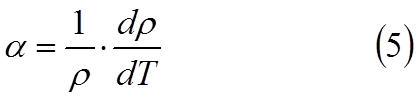Удельное сопротивление данного вещества зависит от его со-стояния, в частности, от температуры. Зависимость удельного со-противления от температуры характеризуется температурным коэффициентом сопротивления (т.к.с.) данного вещества

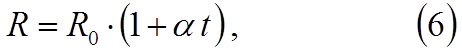Т.к.с. при различных температурах различен. Однако, для многих проводников, к которым относятся все металлы, изменение сопротивления от температуры незначительно. В этом случае для небольшого интервала температур изменение сопро-тивления описывается линейным законом

где  R_o – сопротивление при  0^оС,  R – его значение при  t^oC.  В (6) α  есть средний т.к.с., найденный для определённого интервала температур, в котором можно принять  (6).

Для всех металлов т.к.с. положителен. У всех электролитов и полупроводников, в отличие от металлов, сопротивление при нагревании всегда уменьшается . Сопротивление графита с по-вышением температуры также уменьшается. Для веществ, у которых сопротивление уменьшается с повышением температу-ры, т.к.с. отрицателен.

Качественно зависимость электрического сопротивления от температуры была объяснена классической электронной теори-ей, представлявшей движение заряженных частиц как материаль-ных точек, подчиняющихся законам классической механики.

Для объяснения установленных опытных противоречий в 1924 году была создана новая, так называемая квантовая или волновая механика движения элементарных частиц (в частности – электронов в металлах). На основе квантовых представлений были устранены и опытные противоречия элект-ропроводности.

С основами квантовых представлений теории электрического сопротивления Вы познакомитесь на старших курсах университета.

§ 2. Измерение сопротивления

методом моста

Одним из наиболее точных методов измерения сопротивлений является метод моста. В настоящей работе используется одна из наиболее простых мостовых схем постоянного тока, часто называемая сокращённо мостом Уитстона представляющая собой замкнутый четырёхугольник, составленный из сопротивлений  R , R_x , R₁ , R₂  (см. РИС.1), соединённых между собой проводниками с очень малым сопротивлением. В одну из диагоналей этой схемы включается источник э.д.с. В другую диагональ схемы включается чувствительный гальванометр  G . Эта диагональ схемы и называется мостом в собственном смысле.

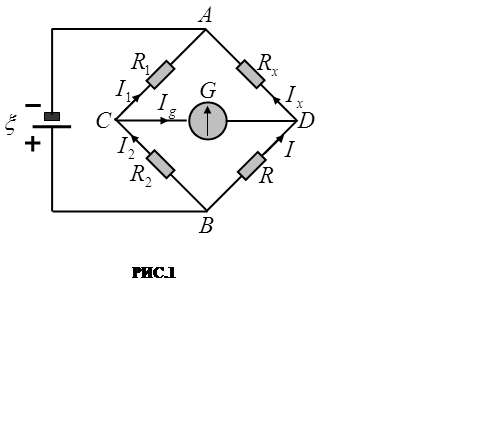Весь процесс измерений при помощи этой схемы свя-зан с требованием равенства нулю тока в мосте  CD.

При произвольном соот-ношении сопротивлений, со-ставляющих всю мостовую схему, через гальванометр, разумеется, должен идти ток (см. РИС.1). Однако, суще-ствует одно определённое соотношение между сопро-тивлениями, составляющими четырёхугольник  CADB, при котором сила тока, идущего через гальванометр, обращается в нуль.

Действительно, на основании закона Ома для однородного участка цепи  CGD , ток на нём равен нулю если потенциалы его концов одинаковы, т.е. φ_А=φ_D:

  

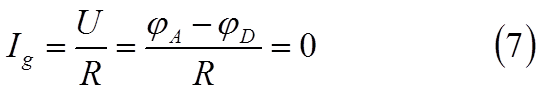
В этом случае  I₁ = I₂   и  I = I_x (нет разветвления токов в узлах  C  и  D).