Изучение резонанса напряжений: Методическое пособие к лабораторной работе № 12

Министерство образования Российской Федерации

ХАБАРОВСКИЙ

ГОСУДАРСТВЕННЫЙ

ПЕДАГОГИЧЕСКИЙ

УНИВЕРСИТЕТ

Кафедра общей физики

Доц. В.Г.Довбило

ЛАБОРАТОРНЫЙ

ПРАКТИКУМ

ПО ЭКСПЕРИМЕНТАЛЬНОЙ

ФИЗИКЕ

 

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

 «ИЗУЧЕНИЕ РЕЗОНАНСА НАПРЯЖЕНИЙ»

Хабаровск 2000

Резонанс напряжений

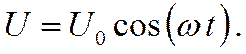Положим, что к цепи, содержащей последовательно соеди-нённые ёмкость С и индуктивность L, обладающую активным со-противлением R (РИС.1), приложено переменное напряжение, из-меняющееся по закону

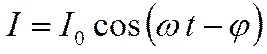Тогда, согласно сказанному в предыдущей лабораторной работе, в цепи будет течь переменный ток

амплитуда которого I_o связана с ам-плитудой напряжения U_o законом Ома для переменного тока

 

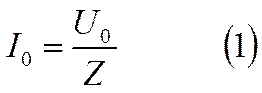Здесь  Z есть полное сопротивление цепи

 

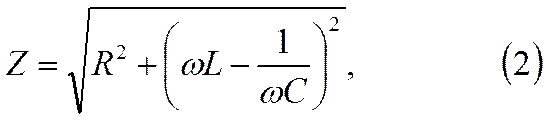а фазовый угол φ, на который колебания тока отстают от колеба-ний напряжения, определяется формулой

 

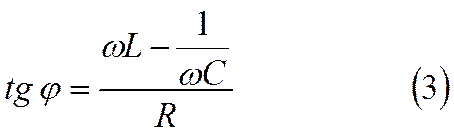Допустим теперь, что мы изменяем частоту колебаний  ω, ём-кость  С  или индуктивность  L . Формулы (1) – (3) показывают, что при этом изменяется и амплитуда тока I_o и cдвиг фазы φ .

В качестве переменного параметра выберем электрическую ёмкость С (проще реализовать на опыте).

Остановимся сначала на изменении амплитуды тока. Если С=0, то  X_C = 1 / (ωC) =∞ .  Тогда сопротивление  Z  обращается в бесконечность, а  I_o  равно нулю. При увеличении ёмкости квадрат реактивного сопротивления

 

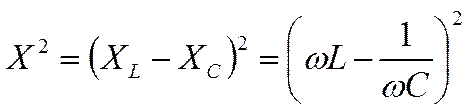
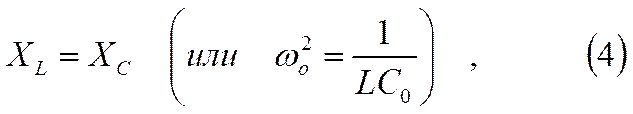сначала уменьшается. Поэтому и сопротивление  Z  уменьшается, а  I_o  увеличивается. При ёмкости конденсатора  С_о , определяе-мой условием

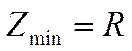реактивное сопротивление  X=X_L-X_C  обращается в нуль, а сопро-тивление  Z  становится наименьшим, равным активному сопро-тивлению цепи

Сила тока при этом достигает максимума.

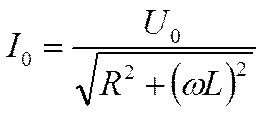При дальнейшем увеличении  С  квадрат реактивного сопротивления снова не равен нулю и возрастает с возрастанием ёмкости. В соответствии с этим, сопротивление  Z увеличивается, а амплитуда тока уменьшается,  асимптотически приближаясь к

Зависимость амплитуды тока I_o от ёмкости С, выражаемая формулами (1) и (2), графически изображена на РИС.1, где пока-заны три кривые, соответствующие трём различным значениям активного сопротивления.

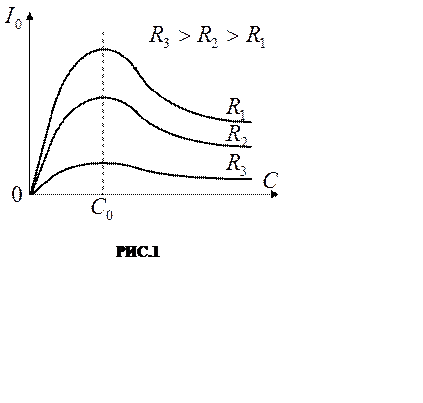Чем меньше активное соп-ротивление контура (т.е., чем меньше декремент затухания  δ или чем больше добротность контура  Q), тем больше, при прочих равных условиях, ам-плитуда тока и тем острее мак-симум кривых.

Обратимся теперь к разнос-ти фаз между током в контуре и приложенным к нему напряже-нием.

Из (3) видно, что при очень малых ёмкостях, когда ωL<<1/ωC,  tgφ  очень велик и отрицателен, а, следовательно, φ=π ∕ 2 . В этом случае ток опережает напряжение и цепь имеет ёмкостный характер. При возрастании ёмкости реактивное сопро-тивление  X=X_L – X_C , оставаясь отрицательным, уменьшается по абсолютной величине и разность фаз φ уменьшается. Когда X_L=X_C , формула (3) даёт tgφ=0, а значит и φ=0 . При дальней-шем увеличении ёмкости реактивное сопротивление цепи стано-вится положительным и увеличивается. Поэтому 0<tgφ<+∞ и 0<φ<+π ⁄  2 .Следовательно, при X_L>X_Cток отстаёт по фазе от напряжения и цепь приобретает индуктивный характер, причём фазовый угол стремится к предельному значению, определяемо-му из условия tgφ=ωL ⁄ R .

Зависимость разности фаз от ёмкости качественно изображе-на графически на РИС.2.

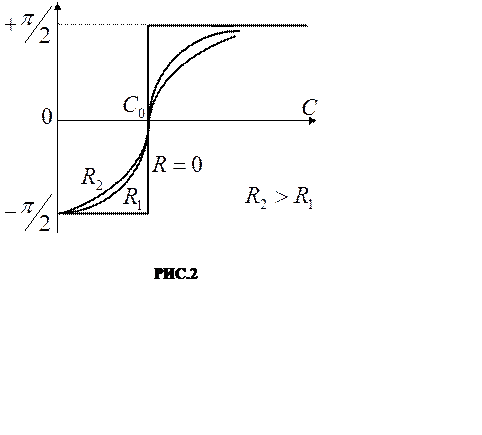Так же как и I_o, φ за-висит ещё и от активного сопротивления контура R Чем меньше R, тем боль-ше изменяется φ вблизи С=С_о, и в предельном случае R=0 изменение фазы приобретает скач-кообразный характер.

Анализируя сказан-ное, мы видим, что осо-бый интерес представля-ет случай, когда реактив-ное сопротивление сопротивление цепи обращается в нуль (X=X_L=X_C=0 или ω²LC=1 или ω=1 ⁄ √LC). При этом амплитуда тока достигает максимального значения, а разность фаз между то-ком и напряжением равна нулю, или, иными словами, контур действует как чисто активное сопротивление. Этот важный слу-чай вынужденных колебаний называется резонансом напряже-ний.

Выше мы предполагали, что изменяется электрическая ём-кость конденсатора С, а индуктивность контура L и частота при-ложенного напряжения ω остаются неизменными. Однако ясно, что для получения резонанса можно поступать и иначе: изменять у контура индуктивность аналогично изменению ёмкости или ча-стоту прилоденного к контуру напряжения.

Отметим, что частота ω_о, при которой наступает резонанс, не равна частоте собственных колебаний контура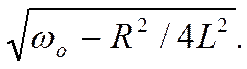 

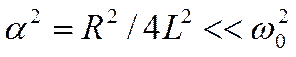Однако, в подавляющем большинстве случаев

и поэтому с хорошим приближением этим различием можно пре-небречь.

Найдём теперь, чему равна амплитуда напряжения на конту-ре и на катушке индуктивности при резонансе.

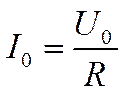Амплитуда тока при резонансе достигает максимума (РИС.1):

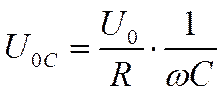Поэтому амплитуда напряжения на конденсаторе

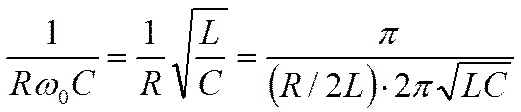Полученное выражение можно записать иначе. Учитывая (4), имеем

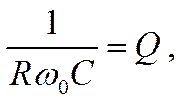Но  R/2L  есть коэффициент затухания α, 2π√LC – период колеба-ния Т, соответствующий резонансу, а значит, знаменатель напи-санной формулы есть логарифмический декремент затухания δ=αТ. Поэтому

где  Q – добротность контура. Следовательно,

 

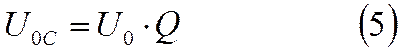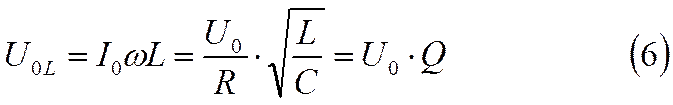Аналогично, амплитуда напряжения на индуктивности есть