Изучение резонанса токов: Методическое пособие к лабораторной работе № 13

Министерство образования Российской Федерации

ХАБАРОВСКИЙ

ГОСУДАРСТВЕННЫЙ

ПЕДАГОГИЧЕСКИЙ

УНИВЕРСИТЕТ

Кафедра общей физики

Доц. В.Г.Довбило

ЛАБОРАТОРНЫЙ

ПРАКТИКУМ

ПО ЭКСПЕРИМЕНТАЛЬНОЙ

ФИЗИКЕ

 

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

«ИЗУЧЕНИЕ РЕЗОНАНСА ТОКОВ»

Хабаровск 2000

Введение

В лабораторных работах №№ 11 и 12 мы рассматривали цепь, в которой активные и реактивные сопротивления были соединены последовательно. Посмотрим теперь, каким образом можно найти соотношение между напряжением и током в цепи параллельного соединения тех же элементов.

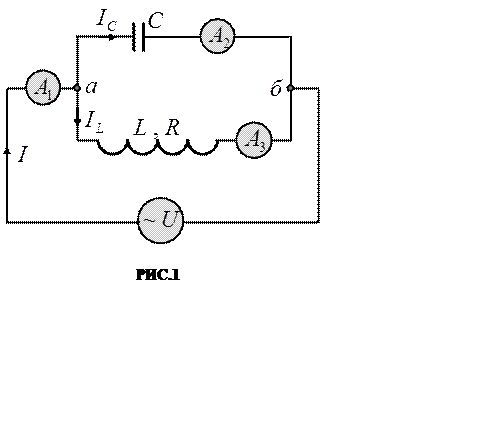
Пусть цепь состоит из двух ветвей (РИС.1):

 К концам цепи а и б приложено напряжение, изме-няющееся по закону

 

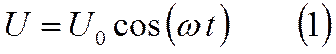Требуется определить ко-лебания силы полного тока I . В случае неразветвлённой цепи общей для всех элементов (L, C, R) была сила тока и задача сводилась к сложению колебаний напря-жения на индуктивности, ёмкости и сопротивлении. Для этой цели мы пользовались векторными диаграммами напряжений.      В этом же случае, напротив, общим является напряжение между точками а и б, а силы тока в ветвях I_C и I_L различны.

Полная сила тока равна

 

и, поэтому, задача сводится к сложению колебаний тока.

Пусть колебание напряжения между точками а и б изображаются вектором, направленным вдоль оси напряжений (РИС.2).

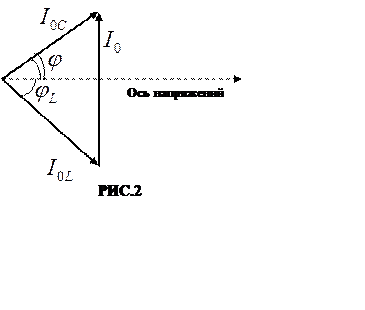
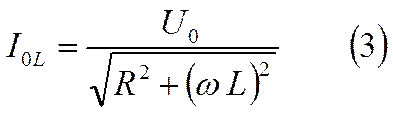Тогда колебания тока в катушке индуктивности изобразятся вектором I_oL .  Его амплитуда равна

Этот вектор повёрнут относительно оси напряжений на угол φ_L  (ток на индуктивности отстаёт по фазе от напряжения), причём

 

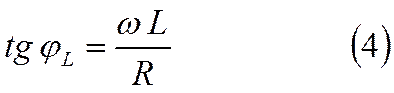Колебания тока в конденсаторе изображаются вектором I_oC , повёрнутым относительно оси напряжений на угол +π/2. Амплитуда этого тока равна

 

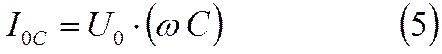Колебания полного тока определяются векторной суммой обоих векторов, т.е. вектором I_o . Его длина есть амплитуда полного тока, а угол φ – угол, на который колебания тока опережают по фазе колебания напряжения.

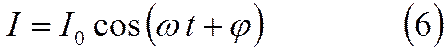Таким образом, колебания полного тока выражаются формулой

Резонанс токов

Если в цепи, изображённой на РИС.1, изменять С, L или частоту генератора ω, то изменяется и амплитуда полного тока и сдвиг фаз между током и напряжением. При некотором соотношении между C, L и ω сдвиг фаз φ становится равным нулю и, следовательно, контур ведёт себя как чисто активное сопротивление. Этот частный случай вынужденных колебаний в разветвлённой цепи называется резонансом токов.

Векторная диаграмма токов, соответствующая резонансу, показана на РИС.3.

Обычно в катушках индуктив-ности ωL>>R  и угол φ_L , согласно (4), очень близок к –π/2. Так как ток I_C в другой ветви опережает напряжение на угол +π/2 , то оба тока I_C и I_L находятся в противофа-зе. Поэтому полный ток I равен приблизительно разности токов I_C и I_L. При резонансе полный ток становится наименьшим (см. РИС.2 и 3), а, следовательно, сопротивление контура достигает наибольшего значения. Это сопротивление, однако, в отличие от резонанса напряжений не равно активному сопротивлению, включённому в контур, а зависит ещё от L и C.

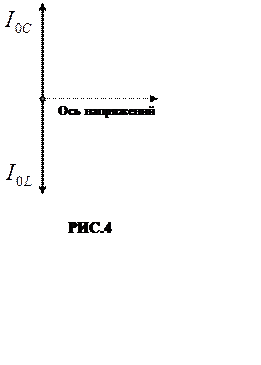Если бы сопротивление R было равно нулю, то разность фаз между токами I_C и I_L была бы точно равна π и оба тока при резонансе точно компенсировали друг друга (РИС.4). В этом случае ток в подводящих проводах был бы равен нулю, хотя каждый из токов I_C и I_L  мог бы иметь весьма большие значения. Сопротивление же контура при резонансе было бы равно бесконечности.

Найдём условие, при котором наступает резонанс токов.

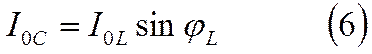Из РИС.3 и 4 видно, что при резонансе токов

но из (4) следует, что

 

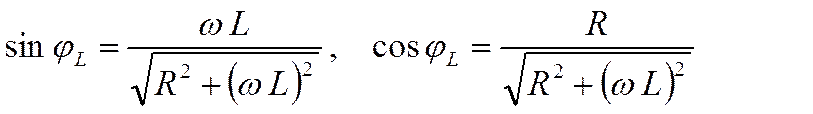Амплитуды же токов I_0C  и I_0L имеют значения

 

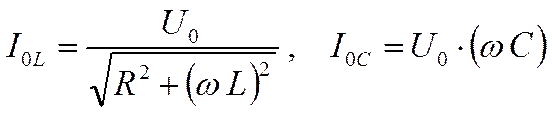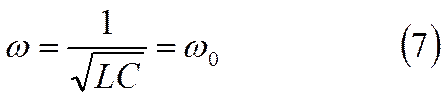Подставляя эти выражения в (6) и считая, что (ωL)² >>R², находим условие резонанса токов

Таким образом, для резонанса токов, так же как и для резонанса напряжений, частота колебаний ω внешнего напряжения должна совпадать с частотой ω_о собственных колебаний контура при отсутствии затуханий.

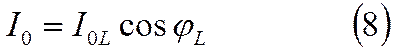Вычислим теперь амплитуду полного тока при резонансе. Из РИС.3 следует, что

При (ωL)² >>R² , имеем

 

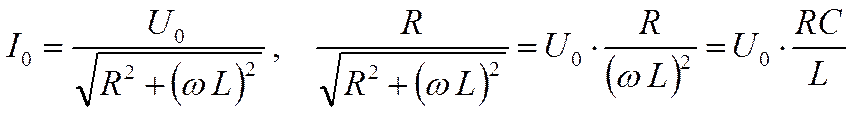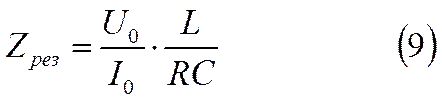Поэтому при резонансе

Если  .

Отношение Z_резконтура к его активному сопротивлению равно квадрату добротности Q контура