Центр масс. Понятие центра масс. Теорема о движении центра масс. Система центра масс (С-система)

ТЕМА7  ЦЕНТР МАСС

1 Понятие центра масс.

2 Теорема о движении центра масс.

3 Система центра масс (С-система).                                                                  

Вопросы для самоподготовки

1 Что понимают под центром масс системы материальных точек?, твердого тела?

2 Может ли центр масс системы находиться в таком месте , где нет никакой материальной точки?

3 Приведите простые примеры экспериментального определения положения центра масс?

4 Существуют ли различия между понятиями центр масс, центр тяжести, центр инерции? Если существуют, то объясните, в чем они заключаются.

5 Какая система отсчета называется системой центра масс? Как принято обозначать эту систему?

6 Чему равен импульс системы материальных точек в системе их центра масс?  

7 Как ведет себя центр масс системы частиц, если импульс системы не изменяется?

8 Система взаимодействующих тел находится в поле силы тяжести вблизи поверхности Земли. Как ведет себя центр масс системы?

9 Является ли система центра масс системы, описанной в вопросе 8, инерциальной?

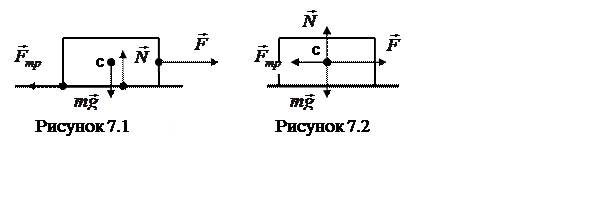
10 Какой из рисунков 7.1 или 7.2, иллюстрирующих движение тела массы m по горизонтальной поверхности под действием внешней силы правильный?

Основные понятия по теме

Пусть имеются n материальных точек, как угодно взаимодействующих между собой и подверженных действию любых внешних сил. Если  радиус-вектор точки номер i , то центром масс (или центром инерции) этой системы материальных точек называется воображаемая точка C, радиус-вектор которой определяется равенством

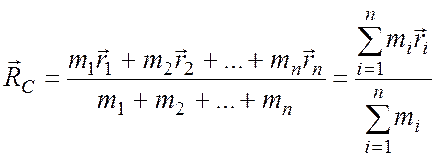                             (7.1)

В случае сплошного тела выражение (7.1) принимает вид

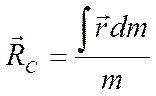,                                                 (7.2)

где масса тела.

В процессе движения материальных точек их радиус-векторы  и радиус-вектор центра масс  в общем случае будут изменяться. Скорость центра масс

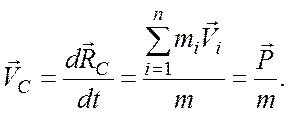                                       (7.3)

Из (7.3) следует, что

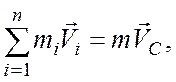                                               (7.4)

т.е. импульс системы материальных точек равен импульсу, который имел бы центр масс, если бы в нем была сосредоточена вся масса системы. Кратко это выражается так: импульс системы равен импульсу центра масс.

Продифференцировав (7.4) по времени, приходим к закону движения центра масс 

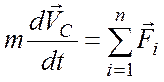.                                               (7.5)

Закон движения центра масс: центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная равнодействующей всех внешних сил, действующих на систему.

Так как импульс замкнутой системы не изменяется, то центр масс замкнутой системы либо движется равномерно и прямолинейно, либо остается неподвижным. Это позволяет связать с ним систему отсчета, которая называется системой центра масс (С-система) и является инерциальной.

Примеры решения задач

1 Определите положение центра масс С плоской однородной фигуры в виде трапеции ABND. Где будет находится центр масс С*, если на эту фигуру наклеить треугольную пластинку ABN из того же материала и такой же толщины так, как показано штриховкой на рисунке 7.3.

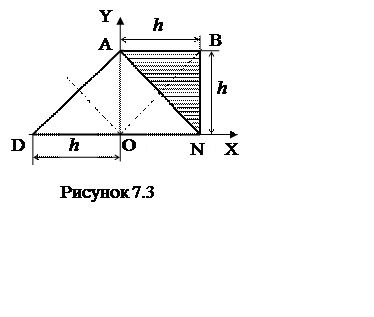Решение. Данная трапеция состоит из квадрата ABNO со стороной h и равнобедренного прямоугольного AOD. Центр масс квадрата находится в точке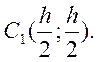  

Рассчитаем координаты центра масс С₂ AOD. Масса треугольника 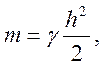 где γ - поверхностная плотность. Уравнение прямой AD

Тогда

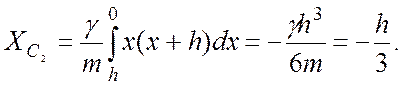
Из соображений симметрии очевидно, что 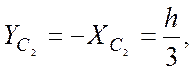 т.е. 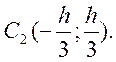 Следовательно, центр масс равнобедренного прямоугольного треугольника находится на биссектрисе прямого угла на расстоянии  от его вершины.

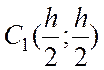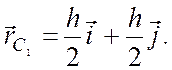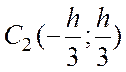Теперь легко найти координаты центра масс С трапеции ABND. Радиус-вектор центра масс  квадрата ABNO, масса которого   Аналогично, для AOD с центром масс  и массой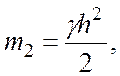 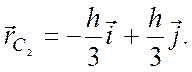  Тогда 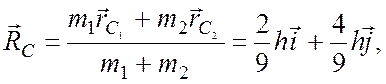 то есть центр масс данной фигуры находится в точке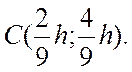

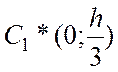При наличии накладки трапецию ABND целесообразно разбить на два треугольника: AND с центром масс  и массой  и ABN такой же массы, для которого 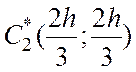 и  В этом случае

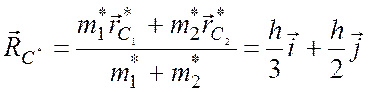  и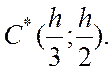 

2 В однородной фигуре, имеющей форму круга радиуса R=30см, вырезано круглое отверстие радиуса r=10см. Центр отверстия смещен относительно центра круга на расстояние l=8см. Определите положение центра масс С полученной фигуры.

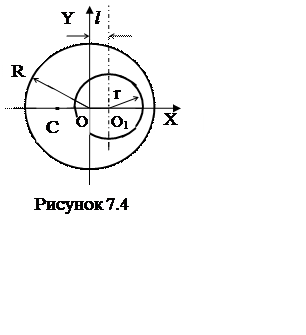Решение. Будем считать, что центр масс данной фигуры расположен в точке С. Положение точки С относительно начала O выбранной системы координат (рисунок 7.4) определяется радиус-вектором

                     (1)

где  и координаты центра масс.

Мысленно вернем удаленную часть фигуры в исходное положение. Тогда радиус-вектор центра масс O₁ возвращенной части

                               (2)

Очевидно, что после возвращения удаленной части, центр масс «реставрированной» фигуры будет расположен в точке O, радиус-вектор которой

                                        (3)