Здесь ![]() масса данной фигуры,
масса данной фигуры, ![]() масса удаленной части, γ – поверхностная
плотность.
масса удаленной части, γ – поверхностная
плотность.
Подставив (1) и (2) в (3), получаем
![]()
Отсюда легко найти
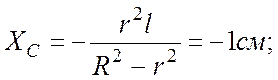
![]()
Следовательно, центр масс данной фигуры расположен на оси OX, что ясно из соображений симметрии, и смещен относительно точки O на 1см влево.
3
Лодка
стоит неподвижно на поверхности озера. На корме и на носу лодки на расстоянииl друг от друга сидят рыболовы. Масса лодки M, массы
людей ![]() и
и![]() Рыболовы меняются
местами. Как и в какую сторону переместится при этом лодка относительно воды?
Сопротивлением воды движению лодки пренебречь.
Рыболовы меняются
местами. Как и в какую сторону переместится при этом лодка относительно воды?
Сопротивлением воды движению лодки пренебречь.
Решение. Будем считать, что центр масс лодки ![]() находится
на одинаковом расстоянии от
находится
на одинаковом расстоянии от![]() каждого из рыболовов.
Совместив с
каждого из рыболовов.
Совместив с ![]() начало отсчета O, для радиус-векторов
лодки и рыболовов в исходном положении можем записать
начало отсчета O, для радиус-векторов
лодки и рыболовов в исходном положении можем записать
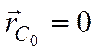 ;
; 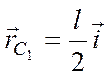 ;
; 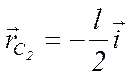 , (1)
, (1)
где ![]() - единичный вектор оси OX.
- единичный вектор оси OX.
Следовательно, радиус-вектор ![]()
![]() центра масс системы лодка-рыболовы в этом
случае
центра масс системы лодка-рыболовы в этом
случае
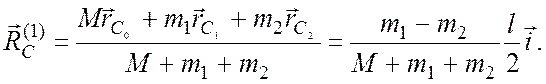 (2)
(2)
Если, после обмена рыболовов местами, центр масс лодки
сместился на величину![]() то выражения аналогичные (1) имеют
вид:
то выражения аналогичные (1) имеют
вид:
![]() ;
; 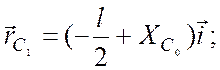
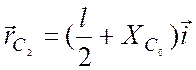
и 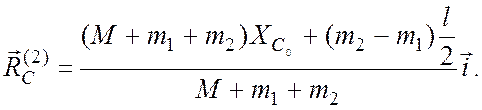 (3)
(3)
Так как система лодка-рыболовы замкнутая, то положение ее центра масс не изменится, т.е.
![]() (4)
(4)
Подставив (2) и (3) в (4), имеем
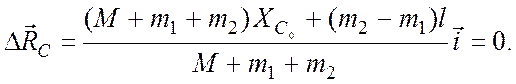
Отсюда
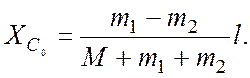
![]()
При ![]() лодка будет смещаться в
направлении оси OX, а при
лодка будет смещаться в
направлении оси OX, а при ![]() в противоположном
направлении.
в противоположном
направлении.
Задачи
1 Система
состоит из трех частиц, массы которых ![]()
![]() и
и ![]() расположенных
в точках А1(1;2;3), А2(2;3;1), А3(3;1;2)
соответственно (значения координат даны в метрах). Найти радиус-вектор
расположенных
в точках А1(1;2;3), А2(2;3;1), А3(3;1;2)
соответственно (значения координат даны в метрах). Найти радиус-вектор ![]() центра масс системы.
центра масс системы.
2 Найти декартовы координаты центра масс С: а) однородной квадратной тонкой пластинки, находящейся в плоскости XY; б) неоднородной квадратной пластинки с поверхностной плотностью σ1=2σ2 , расположенной в той же плоскости (рисунок 7.5 ).
 |
|||
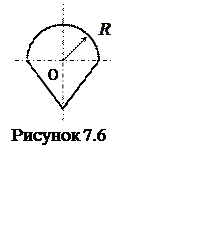 |
3 Однородная фигура состоит из полукруга радиуса R и равностороннего треугольника (рисунок 7.6). Найти координаты ее центра масс С.
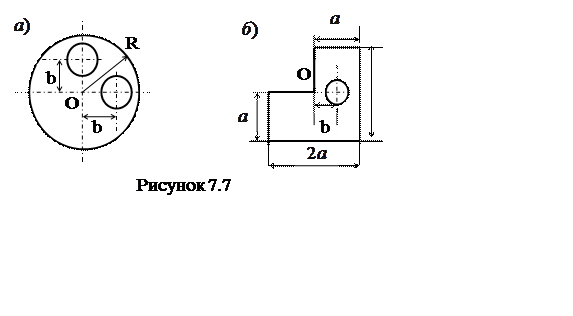
4 Определить положение центра масс однородных плоских фигур, в которых вырезаны круглые отверстия с радиусами r, относительно точки O (рисунок7.7). Необходимые геометрические размеры приведены на рисунках.
 |
5 На какое расстояние сместится неподвижно стоящая на воде лодка, если человек массы m=70кг перейдет с носа лодки на корму? Длина лодки l=2,5м, масса M=100кг. Сопротивлением воды пренебречь.
 6 Через неподвижный блок
перекинута тонкая нерастяжимая нить, на концах которой подвешены грузы массами m1
и m2 (m2 >m1). В
начальный момент времени оба груза находились на одной высоте. Определить, на
какое расстояние сместился центр масс грузов через время t после начала
движения. Найти ускорение центра масс грузов. Трения нет. Массами блока и нити
пренебречь.
6 Через неподвижный блок
перекинута тонкая нерастяжимая нить, на концах которой подвешены грузы массами m1
и m2 (m2 >m1). В
начальный момент времени оба груза находились на одной высоте. Определить, на
какое расстояние сместился центр масс грузов через время t после начала
движения. Найти ускорение центра масс грузов. Трения нет. Массами блока и нити
пренебречь.
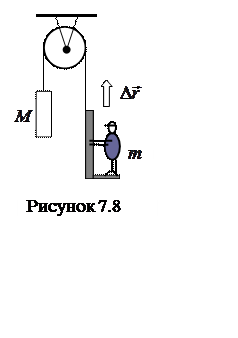
7 Через блок перекинут шнур, на
одном конце которого находится лестница с человеком, а на другом конце –
уравновешивающий груз массы M (рисунок 7.8). Человек, масса которого m,
совершил перемещение ![]() вверх относительно лестницы и
остановился. Пренебрегая массами блока и шнура, найти перемещение центра масс
этой системы.
вверх относительно лестницы и
остановился. Пренебрегая массами блока и шнура, найти перемещение центра масс
этой системы.
8 Система состоит их двух шариков
с массами m1 и m2 , которые
соединены между собой невесомой пружиной. В момент t=0 шарикам сообщили
скорости![]() и
и ![]() , после
чего система начала двигаться в однородном поле тяжести Земли. Пренебрегая
сопротивлением воздуха, найти зависимости от времени импульса этой системы в
процессе движения и радиус-вектора ее центра масс относительно его начального
положения.
, после
чего система начала двигаться в однородном поле тяжести Земли. Пренебрегая
сопротивлением воздуха, найти зависимости от времени импульса этой системы в
процессе движения и радиус-вектора ее центра масс относительно его начального
положения.
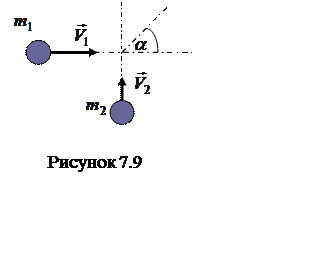
9 Два тела
массами ![]() и
и ![]() скользят
по гладкому горизонтальному столу во взаимно перпендикулярных направлениях
(рисунок 7.9). После неупругого соударения они движутся дальше вместе в
направлении, составляющем угол α с направлением движения первого тела до
столкновения. Найти отношение скоростей тел до удара. Для изображенного на
рисунке 7.9 момента укажите положение центра масс системы и направление его
скорости. Покажите, что сумма импульсов тел в С-системе равна нулю.
скользят
по гладкому горизонтальному столу во взаимно перпендикулярных направлениях
(рисунок 7.9). После неупругого соударения они движутся дальше вместе в
направлении, составляющем угол α с направлением движения первого тела до
столкновения. Найти отношение скоростей тел до удара. Для изображенного на
рисунке 7.9 момента укажите положение центра масс системы и направление его
скорости. Покажите, что сумма импульсов тел в С-системе равна нулю.
 |
|||
 |
|||
10. Два небольших тела, массы которых m1
и m2 , связаны между собой легкой
нерастяжимой нитью длины l. Тела движутся по гладкой горизонтальной
поверхности так, что в некоторый момент времени скорость одного тела равна
нулю, а второго - ![]() , причем ее направление
перпендикулярно нити (рисунок 7.10). Определить силу натяжения нити в процессе
движение тел.
, причем ее направление
перпендикулярно нити (рисунок 7.10). Определить силу натяжения нити в процессе
движение тел.
Ответы и указания
1 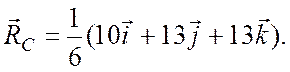
2 a)C(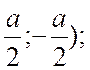 б)
б)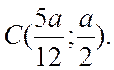
3 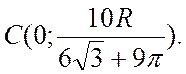
4 а)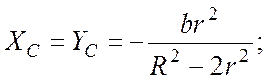 б)
б)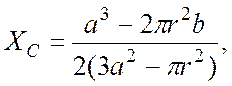
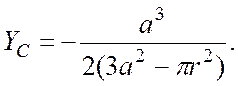
5 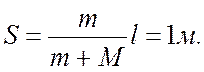
6 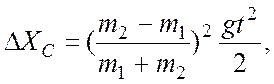
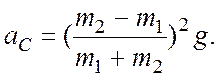
7 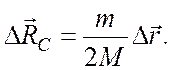 Центр масс системы сместиться вертикально
вверх.
Центр масс системы сместиться вертикально
вверх.
8 1)![]() где
где ![]()
![]()
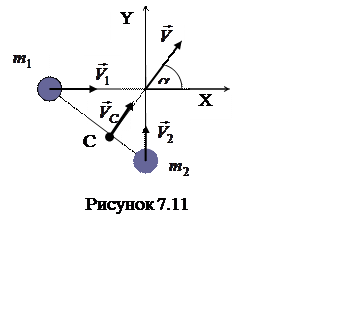 2)
2)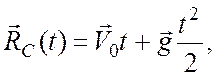 где
где 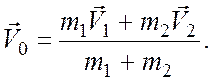
9 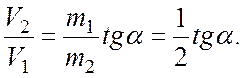
Ответ на второй вопрос задачи очевиден из
построения приведенного на рисунке 7.11.
10 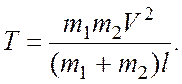
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.