Системы случайных величин. Понятие многомерной случайной величины. Закон распределения двумерной дискретной СВ. Ковариация. Коэффициент корреляции

ЛЕКЦИЯ 5

СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН

5.1. Понятие многомерной случайной величины.. 1

5.2. Закон распределения двумерной дискретной СВ.. 1

5.3. Функция распределения двумерных СВ.. 2

5.4. Непрерывные двумерные СВ. Плотность распределения. 2

5.5. Независимость случайных величин. 3

5.6. Ковариация. Коэффициент корреляции. 4

КОНТРОЛЬНЫЕ ВОПРОСЫ.. 5

5.1. Понятие многомерной случайной величины

            В некоторых случаях результаты эксперимента нельзя описать с помощью одной СВ.

            Пример. 1) Оценка в фигурном катании (x,h), где x - оценка за технику, h - оценка за артистизм.

2) (x, h, m), где x - рост человека, h - вес человека, m - давление человека.

            Совместное рассмотрение нескольких числовых параметров случайного эксперимента приводит к рассмотрению многомерных СВ.

Определение 5.1. Многомерной случайной величиной называется совокупность (x₁, x₂, …, x_n) случайных величин x₁, x₂, …, x_n, заданных под одним и тем же пространством элементарных исходов.

   Значение n – мерной СВ зависит от элементарных исходов W. Если  x₁, x₂, …, x_n дискретны, то n – мерная СВ – дискретна. Если x₁, x₂, …, x_n непрерывны, то n – мерная СВ – непрерывна.

   При n = 2 - двумерная СВ (x₁, x₂). Иногда удобно записывать . Случайную величину (x,h) можно рассматривать как случайную точку на плоскости.

  Если , то СВ  может быть рассмотрена как точка пространства .

  При изучении многомерных СВ ограничимся рассмотрением только двумерной СВ, т. к. все свойства легко обобщаются на случай .

5.2. Закон распределения двумерной дискретной СВ

            Пусть задана дискретная двумерная случайная величина . Если x принимает возможные значения  , h принимает возможные значения , то  принимает возможные значения , где , .

            Обозначим  – вероятность того, что  и . Так как события  образуют полную группу   , то 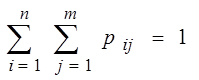. Тогда закон распределения  можно записать в виде таблицы.

            Зная закон распределения двумерной СВ  всегда можно найти закон распределения одномерных СВ x и h. Соответствующие вероятности

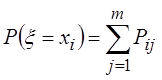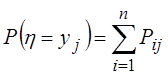, где ,

, где .

         Пример. ДСВ задана законом распределения:

	1	2
-1	0,2	0,1
0	0,3	0,05
1	0,15	0,2

x	-1	0	1
р	0,3	0,35	0,35

h	1	2
р	0,45	0,35

5.3. Функция распределения двумерных СВ

            Универсальной характеристикой многомерных СВ, пригодной для дискретных и непрерывных СВ является функция распределения.

            Определение 5.2. Функция распределения двумерной СВ – функция вида

,

где .

Функция распределения   – вероятность того, что x примет значение меньше , h – меньше .

            Геометрически функция распределения  представляет собой вероятность попадания случайной точки  в левый нижний бесконечный квадрат плоскости с вершиной в точке .

            Пример. Построить функцию распределения двумерной СВ

	(-∞;1]	[1;2]	[2;+∞)
(-∞;-1]	0	0	0
(-1;0]	0	0,1	0,3
(0;1]	0	0,5	0,65
(1;+∞)	0	0,65	1

Свойства функции распределения

1.   неубывающая по каждому из своих аргументов, т. е.   

, .

2. 

3. 

 

4.   непрерывна слева по каждому из своих аргументов.

5.   , .

5.4. Непрерывные двумерные СВ. Плотность распределения.