Системы случайных величин. Понятие многомерной случайной величины. Закон распределения двумерной дискретной СВ. Ковариация. Коэффициент корреляции, страница 2

            Если функция распределения  непрерывна и имеет непрерывную смешанную производную второго порядка 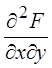, то – непрерывная СВ с двумерной плотностью распределения

.

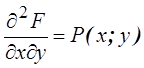Свойства плотности распределения:

1. 

2. 

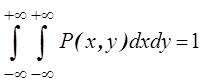
3. 

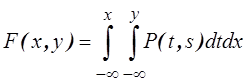
4.

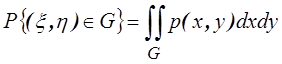
5. ,  .

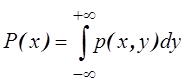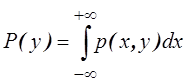         Пример. Известна плотность вероятности двумерной СВ

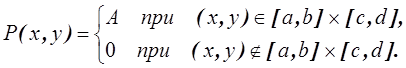
Найти 1) константу , 2) , 3) .

Решение.

1) Из условия нормировки 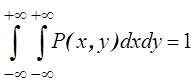 имеем

.

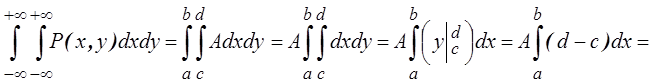
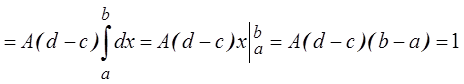Отсюда  .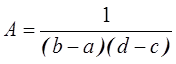

Тогда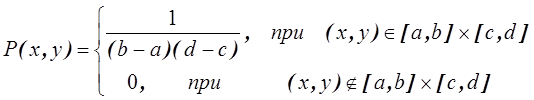

2) Находим плотности распределения одномерных случайных величин

.

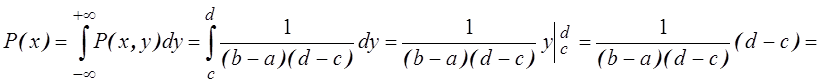
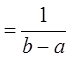Отсюда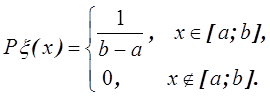 

Аналогично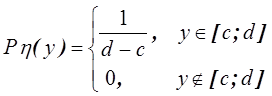

3)

.

5.5. Независимость случайных величин

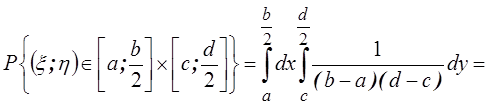
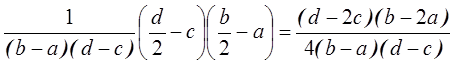            Определение 5.3. Двумерная случайная величина  называются независимыми, если для любых действительных чисел x и y справедливо равенство

.

Из определения следует, что если  дискретная СВ, то .

Если  непрерывная СВ, то .

         Пример. Двумерная случайная величина  задана плотностью вероятности

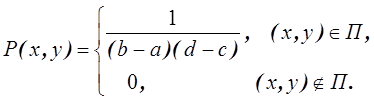
Проверить, являются ли случайные величины  и  независимыми.

Решение. Плотности вероятностей одномерных случайных величин имеют вид

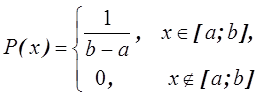 и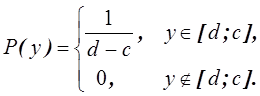

 Очевидно, что  и - независимы.

Пример. Двумерная дискретная случайная величина задана законом распределения

	5	6
1	0,1	0,4
2	0,2	0,3

Проверить, являются ли случайные величины  и  независимыми.

Решение. Одномерные законы распределения случайных величин  и  имеют вид

	1	2
	0,5	0,5

	5	6
	0,3	0,7

С одной стороны . С другой стороны , . Отсюда заключаем, что  и  зависимыми.

5.6. Ковариация. Коэффициент корреляции.

            Определение 5.4. Ковариацией случайных величин   и  называется число

.

            Данная формула для дискретных СВ имеет вид:

,

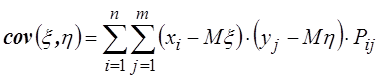для непрерывных СВ:

.

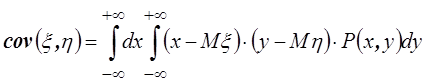            Ковариация характеризует рассеивание СВ  и , а также их взаимное влияние. Поэтому ее иногда называют моментом связи или корреляционным моментом.

Свойства ковариации.

1. .

2.  где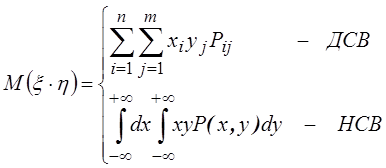

3. Если СВ  и  независимы, то .

Обратное неверно.

            Определение 5.5. Коэффициентом корреляции называется число

,

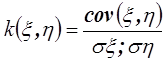где ,  .

            Если ,  , то коэффициент корреляции  не существует.

Свойства коэффициента корреляции.

1.  .

2.  Если  и  линейно зависимы, т. е. , где ,  – числа, то .

           Определение 5.6  Случайные величины  и  называются некоррелируемыми, если . Случайные величины  и  называются коррелируемыми, если .

           Коэффициент корреляции определяет степень линейной вероятностной зависимости между случайными величинами  и . Это проявляется в том, что при возрастании одной СВ другая тоже возрастает; при убывании – другая тоже убывает.

            Пример. Найти коэффициент корреляции СВ.

Решение. Находим одномерные законы распределения и их числовые характеристики.:

, , .

, , .

Тогда

.

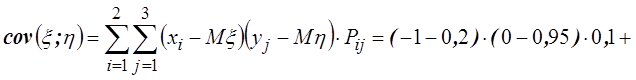
Тогда 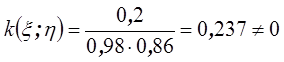. Отсюда следует, что случайные величины  и  коррелируемы, т.е. взаимосвязаны.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Приведите примеры количественных характеристик событий.
2. Дайте определение двумерной дискретной случайной величины. Как получить законы одномерные законы распределения из двумерного закона распределения?
3. Дайте определение функции распределения двумерной случайной величины и перечислите ее свойства.
4. Дайте определение непрерывной двумерной случайной величины и перечислите ее свойства.
5. Какие случайные величины называются независимыми?
6. Дайте определение ковариации и перечислите ее свойства. Что называется коэффициентом корреляции и что он характеризует?