ТЕМА 2 КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
1 Виды движения твердого тела.
2Угловые кинематические величины.
3Связь линейных и угловых кинематических величин.
Вопросы для самоподготовки
1 Что такое центральный угол? В каких единицах он измеряется? Дайте определение единицы измерения центрального угла.
2 Перечислите виды движения твердого тела. Чем отличаются вращение твердого тела вокруг неподвижной оси и вокруг неподвижной точки?
3 Что понимают под плоским движением твердого тела?
4 Обоснуйте целесообразность введения угловых кинематических величин.
5 Дайте определение угловой скорости. Как направлен вектор угловой скорости и чему равен его модуль?
6 Что характеризует угловое ускорение? Как направлен вектор углового ускорения и чему равен его модуль, если ось вращения неподвижна? Если ось вращения поворачивается?
7 Изобразите на рисунке векторы соответствующие углу поворота, угловой скорости и угловому ускорению для твердого тела вращающегося вокруг неподвижной оси. Какой смысл вкладывают в понятие «аксиальный вектор»?
8 Почему понятия периода и частоты вращения вводятся только для равномерного вращательного движения?
9 Объясните различия в формулах ![]() и
и ![]() ,
связывающих линейную и угловую скорости.
,
связывающих линейную и угловую скорости.
10 Запишите формулы выражающие тангенциальное ![]() и нормальное
и нормальное ![]() ускорения
через соответствующие угловые величины.
ускорения
через соответствующие угловые величины.
Основные понятия по теме
При описании вращательного движения в кинематике
удобно пользоваться угловыми кинематическими величинами: ![]()
![]() и
и ![]()
Угловое перемещение ![]() вектор, модуль которого равен углу поворота тела за
время
вектор, модуль которого равен углу поворота тела за
время ![]() Вектор
Вектор ![]() направлен
по оси вращения, а его ориентация, по договоренности, определяется правилом
правого винта.
направлен
по оси вращения, а его ориентация, по договоренности, определяется правилом
правого винта.
Угловая скорость
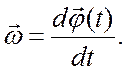 (2.1)
(2.1)
Вектор
![]() направлен вдоль оси вращения так же как и
вектор
направлен вдоль оси вращения так же как и
вектор ![]() то есть по правилу правого винта.
то есть по правилу правого винта.
Угловое ускорение
 (2.2)
(2.2)
показывает,
как быстро изменяется вектор угловой скорости. Вектор ![]() направлен
вдоль оси вращения в сторону вектора приращения угловой скорости (при
ускоренном вращении вектор
направлен
вдоль оси вращения в сторону вектора приращения угловой скорости (при
ускоренном вращении вектор ![]() сонаправлен вектору
сонаправлен вектору ![]() а при замедленном – противоположен ему).
Ориентация векторов
а при замедленном – противоположен ему).
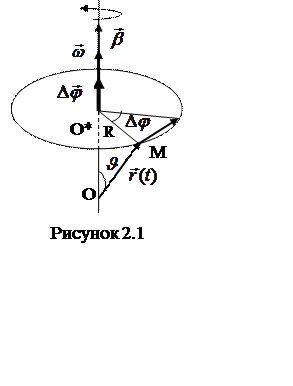
Ориентация векторов ![]()
![]() и
и ![]() (для случая ускоренного вращения) показана
на рисунке 2.1.
(для случая ускоренного вращения) показана
на рисунке 2.1.
|
При равномерном вращении
![]()
![]()
![]() (2.3)
(2.3)
Дополнительно равномерное вращение характеризуется периодом вращения и частотой.
Период вращения ![]() время,
за которое тело совершает один полный оборот.
время,
за которое тело совершает один полный оборот.
Частота вращения ![]() число
оборотов совершаемых телом в единицу времени.
число
оборотов совершаемых телом в единицу времени.
Период, частота , угловая скорость связаны очевидными соотношениями
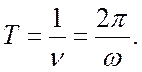 (2.4)
(2.4)
При равноускоренном вращении
![]()
![]()
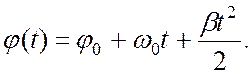 (2.5)
(2.5)
Линейные и угловые кинематические величины связаны соотношениями
![]()
![]() (2.6)
(2.6)
![]()
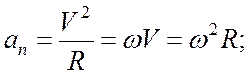 (2.7)
(2.7)
![]()
![]() . (2.8)
. (2.8)
Здесь ![]() радиус – вектор точки М
(рисунок 2.1),
радиус – вектор точки М
(рисунок 2.1), ![]() радиус окружности по которой
движется точка М. Заметим, что
радиус окружности по которой
движется точка М. Заметим, что ![]() и
и ![]() являются полярными координатами точки М с
полюсом О* лежащим на оси вращения.
являются полярными координатами точки М с
полюсом О* лежащим на оси вращения.
Примеры решения задач
 |
1 Шкив радиусом ![]() приводится во вращение с помощью
намотанной на него веревки, конец которой тянут с ускорением
приводится во вращение с помощью
намотанной на него веревки, конец которой тянут с ускорением ![]() (рисунок 2.2). Найти нормальное
(рисунок 2.2). Найти нормальное ![]() , тангенциальное
, тангенциальное ![]() и
полное
и
полное ![]() ускорения нижней точки А шкива и
определить ее положение спустя время
ускорения нижней точки А шкива и
определить ее положение спустя время ![]() после начала вращения.
после начала вращения.
Решение. Для
точки В, как и для всех точек лежащих на ободе шкива, ускорение ![]() является тангенциальным, то есть
является тангенциальным, то есть ![]() . Следовательно угловое ускорение шкива
. Следовательно угловое ускорение шкива
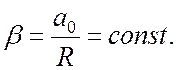
Так как шкив вращается равноускоренно без начальной скорости, то его угловая скорость в момент времени t
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.