Тема 1Кинематика материальной точки
1 Задачи кинематики.
2 Способы описания движения материальной точки.
3 Законы движения.
4 Тангенциальное, нормальное и полное ускорения.
Вопросы для самоподготовки
1 Сформулируйте основную задачу кинематики.
2 Перечислите способы описания движения материальной точки. Кратко охарактеризуйте их достоинства и недостатки.
3 В чем состоит векторный способ описания движения? Каков физический смысл радиус-вектора?
4 Чем отличается вектор перемещения точки от пути? При каких условиях длина вектора перемещения будет равна пути, проходимому точкой?
5 Что называют вектором мгновенной скорости? Где расположено начало этого вектора и как он направлен в пространстве?
6 Что называют вектором мгновенного ускорения точки и каков его физический смысл? Как направлен этот вектор? Почему его направление не совпадает при криволинейном движении с направлением скорости?
7 Что такое тангенциальное ускорение? Что оно характеризует при криволинейном движении? Как направлен вектор тангенциального ускорения и чему равен его модуль?
8 Что называют вектором нормального ускорения и что он характеризует? Каким выражением определяется его модуль?
9 Что такое радиус кривизны траектории? Почему малый участок траектории можно приближенно считать дугой некоторой окружности и что это за окружность?
10 Может ли полное ускорение при криволинейном движении быть направленным по касательной к траектории? По нормали к траектории?
Основные понятия по теме
В механике для описания движения материальной точки используют три способа: векторный, координатный и естественный. В наиболее общем векторном способе положение точки М относительно точки О, принятой за точку отсчета, определяется радиус-вектором
![]() (1.1)
(1.1)
проведенным из точки О в точку М (рисунок 1.1). Выражение (1.1) называют законом движения точки в векторной форме.
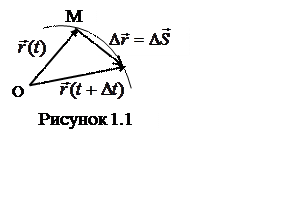 В этом
случае траекторией точки является линия, описываемая концом
радиус-вектора, а изменение радиус-вектора
В этом
случае траекторией точки является линия, описываемая концом
радиус-вектора, а изменение радиус-вектора
![]() (1.2)
(1.2)
определяет вектор перемещения ![]() точки
М за время
точки
М за время ![]()
В координатном способе с точкой отсчета О
связывают начало выбранной системы координат. Чаще всего используют декартову
систему координат, ортонормированный базис которой образован тремя единичными
по модулю и взаимно ортогональными векторами ![]()
![]()
![]() задающими направления
осей X, Y, Z (рисунок 1.2). В этом случае радиус-вектор
задающими направления
осей X, Y, Z (рисунок 1.2). В этом случае радиус-вектор
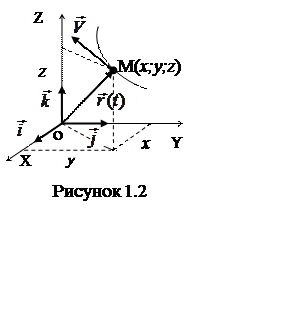
![]() (1.3)
(1.3)
и положение точки М в момент времени t определяется ее координатами
![]()
![]()
![]() (1.4)
(1.4)
то есть проекциями радиус-вектора на координатные оси. Уравнения (1.4) называют кинематическими уравнениями движения материальной точки или законами движения точки в координатной форме.
Соответственно вектор перемещения точки![]()
![]() (1.5)
(1.5)
где
![]()
![]() и
и ![]() изменение координат точки за время
изменение координат точки за время ![]()
Уравнение траектории точки можно получить, исключив время из системы кинематических уравнений движения (1.4).
Для того чтобы охарактеризовать как быстро изменяется положение точки в пространстве и кинематике вводится понятие скорости.
Скорость- это векторная величина, которая определяет как быстроту движения, так и его направление в данный момент.
Вектором средней скорости ![]() за интервал времени
за интервал времени ![]() называется
отношение приращения
называется
отношение приращения ![]() радиус-вектора точки к
промежутку времени
радиус-вектора точки к
промежутку времени ![]()
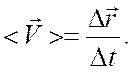 (1.6)
(1.6)
Мгновенная скорость
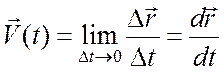 .
(1.7)
.
(1.7)
Вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки (рисунок 1.2).
В координатном способе описания вместо вектора
мгновенной скорости ![]() используют его проекции на
координатные оси
используют его проекции на
координатные оси
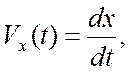
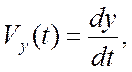
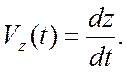 (1.8)
(1.8)
В этом случае модуль мгновенной скорости
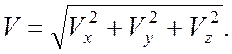 (1.9)
(1.9)
В общем случае модуль мгновенной скорости равен первой производной пути по времени
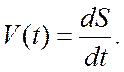 (1.10)
(1.10)
При неравномерном движении модуль мгновенной скорости
изменяется. В связи с этим вводят скалярную величину ![]() среднюю
скорость неравномерного движения. Очень часто эту величину называют средней
путевой скоростью.
среднюю
скорость неравномерного движения. Очень часто эту величину называют средней
путевой скоростью.
Выражения аналогичные (1.6)-(1.10) имеют место и для ускорения
![]() векторной величины, характеризующей
быстроту изменения скорости по модулю и направлению.
векторной величины, характеризующей
быстроту изменения скорости по модулю и направлению.
Вектор среднего ускорения
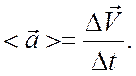 (1.11)
(1.11)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.