ЛАБОРАТОРНАЯ РАБОТА №6
ИЗУЧЕНИЕ ЯВЛЕНИЯ ТЕРМОЭЛЕКТРОННОЙ ЭМИССИИ С ПОМОЩЬЮ ВАКУУМНОГО ДИОДА.
ЦЕЛЬ Исследование ВАХ вакуумного диода, прповерка закона Богуславского - Ленгмюра и определение удельного заряда электрона. Экспирементальное иэучение зависимости плотности тока насыщени я от температуры катода и определение работы выхода электрона на основании уравнения Зичардсона-Дешмена.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Как свидетельствуют экспериментальные данняе, электроны в
метале могут иметь только некоторые, вполне вполне определённые значения
энергии.При этом состояние электрона в металле можно описать с помощью системы
энергитических уровней или дискретного энергитического спектра (рис. 6.1).
Каждому возможномусостоянию электрона, характерезуемому определённой энергией ![]() , соответствует некоторый энергитический
уровень и наоборот. Распределение электронов по возможным кавантовым состояниям
описывается статистикой Ферми-Дирака, согласно которой вероятность заполнения
состояния с энергией
, соответствует некоторый энергитический
уровень и наоборот. Распределение электронов по возможным кавантовым состояниям
описывается статистикой Ферми-Дирака, согласно которой вероятность заполнения
состояния с энергией ![]() определяется
функцией
определяется
функцией
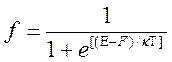 (6.1)
(6.1)
Где
![]() – постоянная Больцмана,
– постоянная Больцмана, ![]() - абсолютная температура, F- некоторое
характерное значение энергии, называемое электрохимическим потанциалом или
уровнем Ферми. С целью выяснения физического смысла постоянной F
рассмотрим поведение функции Ферми-Дирака при абсолютном нуле температур.
Пологая T=0 в выражении (6.11), получаем
- абсолютная температура, F- некоторое
характерное значение энергии, называемое электрохимическим потанциалом или
уровнем Ферми. С целью выяснения физического смысла постоянной F
рассмотрим поведение функции Ферми-Дирака при абсолютном нуле температур.
Пологая T=0 в выражении (6.11), получаем ![]() при Е<F и
при Е<F и ![]() при E>F . Зависимость
при E>F . Зависимость ![]() (6.1) при T=0 имеет вид разрывной
ступенчатой функции и представлена на рисунке 6.2 кривой 1. Таким образом при
абсолютном нуле температур все без исключения энергетические , лежащие нмже
уровня Ферми, заняты электронами. В то же время все квантовые состояния,
энергия которых больше энергии Ферми, полностью свободны. Наличие такой резкой
границы между занятыми и свободными энергитическими уровнями обьясняется тем,
что при T=0 реализуется основное состояние твердого тела, т.е.
состояние с наименьшей возможной энергией. При этом количество заполненых
квантовых состояний равно количеству электпронов в метале, поскольку в
соответствии с принципом запрета Паули в каждом квантовом состоянии может
находится не более одного электрона.
(6.1) при T=0 имеет вид разрывной
ступенчатой функции и представлена на рисунке 6.2 кривой 1. Таким образом при
абсолютном нуле температур все без исключения энергетические , лежащие нмже
уровня Ферми, заняты электронами. В то же время все квантовые состояния,
энергия которых больше энергии Ферми, полностью свободны. Наличие такой резкой
границы между занятыми и свободными энергитическими уровнями обьясняется тем,
что при T=0 реализуется основное состояние твердого тела, т.е.
состояние с наименьшей возможной энергией. При этом количество заполненых
квантовых состояний равно количеству электпронов в метале, поскольку в
соответствии с принципом запрета Паули в каждом квантовом состоянии может
находится не более одного электрона.
Если температура металла отлична от нуля, то электроны вследствии хаотического
теплового движения могут заполнять энергитические уровни, лежащие выше уровня Ферми.
Функция распределения(6.1 становится непрерывной. График зависимости ![]() представлен на рисунке (6.2)кривой 2. При достаточно больших удовлетворяющих
условию E-F>>
представлен на рисунке (6.2)кривой 2. При достаточно больших удовлетворяющих
условию E-F>>![]() , функция (6.1) принимает вид
, функция (6.1) принимает вид
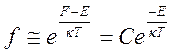 (6.2)
(6.2)
Т.е. распределение Ферми-Дирака переходит в класическое распредиление Больцмана.
Выражение(6.2) справедливо также для электпронов,покинувших металл и
находящихся в термодинамическом равновесии с электронным газом, существующим
внутри металла. Пусть электрон, покоящийся за пределами металла вблизи его
поверхности, имеет энергию ![]() .
Тогда с помощью функции(6.2) можно найти вероятность выхода электрона за
поверхность
.
Тогда с помощью функции(6.2) можно найти вероятность выхода электрона за
поверхность
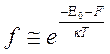 (6.3)
(6.3)
Как
свидетельствует выражение (6.3), вероятность эмиссии электронов отлична от нуля
и быстро увеличивается с ростом температуры. Образование электронного облака
вблизи поверхности металла вследствии теплового движения электронов называется
термоэлектронной эмиссией. Основной величиной, характеризующей интенсианость
термоэлектронной эмиссии, является так называемая работа выхода ![]() . Это энергия необходимая для перевода электрона с
уровня Ферми за пределы металла (см. рис. 6.3). Для чистых металлов
термоэлектронная работа выхода имеет порядок несколько эВ. При возрастании
работы выхода интенсивность тэрмоэлектронной эмиссии и плотность электронного
облака вблизи поверхности металла резко уменьшается в соответствии с выражением
(6.3).
. Это энергия необходимая для перевода электрона с
уровня Ферми за пределы металла (см. рис. 6.3). Для чистых металлов
термоэлектронная работа выхода имеет порядок несколько эВ. При возрастании
работы выхода интенсивность тэрмоэлектронной эмиссии и плотность электронного
облака вблизи поверхности металла резко уменьшается в соответствии с выражением
(6.3).
Электрическое поле, сууществующее внутри вакуумного диода, в соответствии с
принципом суперпозиции обусловлено, с одной стороны, разностью потанциалов
между электронами, и с другой- наличием пространственного заряда в обяеме
электронной лампы. Разделение электрического потанциала ![]() между анодом и катодом можно описать с помощью
уравнения Пуасона
между анодом и катодом можно описать с помощью
уравнения Пуасона
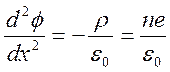 (6.4)
(6.4)
Где
![]() - обьёмная плотность пространственного заряда, n -
концентрация электронов, e- элементарный электрический заряд. С целью упрощения
задачи рассматриваются электроды, ось X направлена перпендикулярно их
поверхности, начало координат совмещено с катодом. Вэтом случае зависимость
всех величин от координат Y и Z можно
пренибречь, и поэтому уравнение(6.4) записано в одномерной форме. Обьёмная
плотность электрического тока в любой точке внутри диода определяется
выражением
- обьёмная плотность пространственного заряда, n -
концентрация электронов, e- элементарный электрический заряд. С целью упрощения
задачи рассматриваются электроды, ось X направлена перпендикулярно их
поверхности, начало координат совмещено с катодом. Вэтом случае зависимость
всех величин от координат Y и Z можно
пренибречь, и поэтому уравнение(6.4) записано в одномерной форме. Обьёмная
плотность электрического тока в любой точке внутри диода определяется
выражением
![]() (6.5)
(6.5)
Где![]() – скорость упорядоченого движения
электрона от катода к аноду (скорость дрейфа). Эта скорость может быть найдена
из закона сохранения энергии
– скорость упорядоченого движения
электрона от катода к аноду (скорость дрейфа). Эта скорость может быть найдена
из закона сохранения энергии
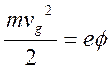 (6.6)
(6.6)
Согласно которому кинетическая энергия упорядоченого движения электронов обусловлена их ускорением в электронном поле, существующем в пространстве между электродами. В результате использования соотношений (6.5),(6.6) уравнение Пуасона (6.4) можно переписать в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.