ЛАБОРАТОРНАЯ РАБОТА №2
ИСПОЛЬЗОВАНИЕ КОНДЕНСАТОРА В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Краткие сведения из теории.
К заданию1
Отличие квазистационарных токов от постоянного тока в том, что изменение тока происходит достаточно медленно, так, что в каждый момент времени для электрических величин, описывающих состояние системы, выполняются все закономерности, характерные для постоянного тока. Процессы зарядки и разрядки конденсатора, в этом смысле, можно отнести к квазистационарным.

Эти процессы проиллюстрированы на схеме.
Рассмотрим процесс зарядки. Ключ замыкается в верхнее положение (1). По правилу
Кирхгофа для верхнего контура ![]() , где Iз – мгновенный
ток зарядки, U – мгновенное значение напряжения на конденсаторе.
Напряжение на конденсаторе и зарядный ток соответственно равны:
, где Iз – мгновенный
ток зарядки, U – мгновенное значение напряжения на конденсаторе.
Напряжение на конденсаторе и зарядный ток соответственно равны: 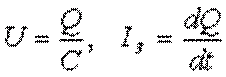 .
.
Выразив ток через напряжение, подставив в
первую формулу и преобразовав ее, получаем следующее выражение: 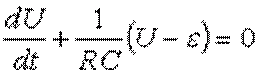
Решаем его относительно мгновенного значения напряжения
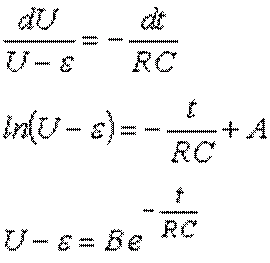
где A и ![]() – некоторые константы. Из начального условия
– некоторые константы. Из начального условия ![]() можно определить
можно определить ![]() . Тогда выражения для
мгновенного напряжения на конденсаторе и мгновенного тока в контуре примут вид:
. Тогда выражения для
мгновенного напряжения на конденсаторе и мгновенного тока в контуре примут вид:
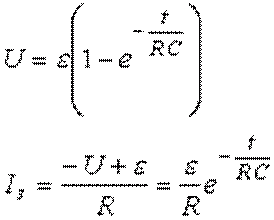 .
.
Видно, что в момент замыкания ключа ток
практически мгновенно достигает значения 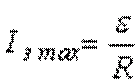 , а потом по экспоненциальному закону спадает до
нуля при
, а потом по экспоненциальному закону спадает до
нуля при ![]() . При разрядке
конденсатора через сопротивление наблюдаются следующие закономерности. В момент
замыкания ключа в нижнее положение (2) в цепи потечет ток, вызванный наличием
напряжения на обкладках конденсатора
. При разрядке
конденсатора через сопротивление наблюдаются следующие закономерности. В момент
замыкания ключа в нижнее положение (2) в цепи потечет ток, вызванный наличием
напряжения на обкладках конденсатора 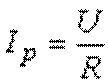 При этом мгновенные значения тока и напряжения
будут равны:
При этом мгновенные значения тока и напряжения
будут равны: 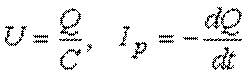
Знак "–" в формуле для тока
показывает, что выбранное положительное направление тока соответствует
уменьшению заряда конденсатора. Эта система уравнений решаются аналогично
случаю зарядки конденсатора. Получается выражение: 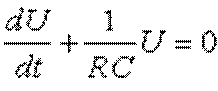 , откуда
, откуда  . Опять же из начальных условий
. Опять же из начальных условий ![]() определяется
определяется ![]() , и формула мгновенного напряжения на обкладках
конденсатора принимает окончательный вид:
, и формула мгновенного напряжения на обкладках
конденсатора принимает окончательный вид:  . Мгновенный ток, как в случае зарядки, так и в
случае разрядки конденсатора определяется формулой:
. Мгновенный ток, как в случае зарядки, так и в
случае разрядки конденсатора определяется формулой:
 .
.
Из приведенных выше рассуждений видно, что
зарядка и разрядка конденсатора происходит не мгновенно, а в течение некоторого
времени. Скорость установления напряжения на конденсаторе зависит от R и C.
Величина, постоянная для данного контура, ![]() называется постоянной времени данного контура (или
временем релаксации) и показывает, через какое время после выключения
называется постоянной времени данного контура (или
временем релаксации) и показывает, через какое время после выключения ![]() напряжение на конденсаторе
уменьшится в e = 2,71 раза.
напряжение на конденсаторе
уменьшится в e = 2,71 раза.
К заданию 3
Пример последовательного соединения RС элементов показан на рис. 1.

Рис. 1
Произведем анализ процессов, протекающих в схеме рис.
1. Определим параметр емкостного сопротивления: 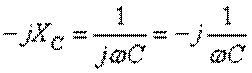 . Затем определим комплекс общего
сопротивления цепи между точками 1 и 2.
. Затем определим комплекс общего
сопротивления цепи между точками 1 и 2. 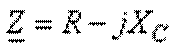 или в показательной форме записи:
или в показательной форме записи: 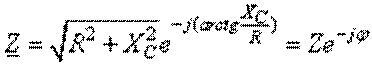 . Величина
. Величина 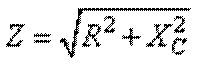 называется комплексом
сопротивления, а величина
называется комплексом
сопротивления, а величина 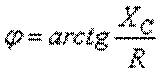 фазой или углом нагрузки. На комплексной плоскости
сопротивление
фазой или углом нагрузки. На комплексной плоскости
сопротивление ![]() будет
выглядеть следующим образом (рис. 2 а):
будет
выглядеть следующим образом (рис. 2 а):

Рис. 2.
Если ток, протекающий по цепи, равен ![]() , тогда напряжение
, тогда напряжение 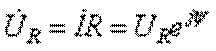 , напряжение на катушке
индуктивности
, напряжение на катушке
индуктивности 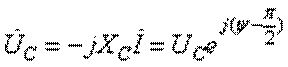 .
Напряжение, приложенное к цепи, будет равно:
.
Напряжение, приложенное к цепи, будет равно: ![]() .
.
К заданию 4
Пример параллельного соединения RC элементов показан на рис. 3.

Рис. 3.
Определим ток в сопротивлении 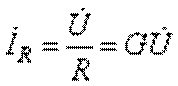 , а ток через емкость равен
, а ток через емкость равен 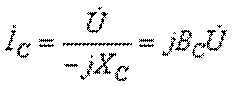 .
.
Определим общую проводимость цепи между точками 1 и 2:
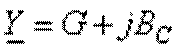 или в
показательной форме записи:
или в
показательной форме записи: 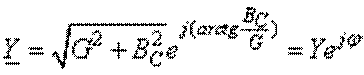 . Комплекс общего сопротивления между
точками 1 и 2 можно определить по формуле:
. Комплекс общего сопротивления между
точками 1 и 2 можно определить по формуле: 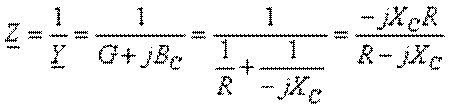 .
.
Комплекс тока, потребляемого схемой из источника,
определим как: 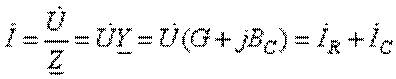 .
.
Положение вектора проводимости ![]() на комплексной плоскости показано
на рис. 4 а. Если напряжение, приложенное к цепи равно
на комплексной плоскости показано
на рис. 4 а. Если напряжение, приложенное к цепи равно ![]() , тогда ток, протекающий через
сопротивление
, тогда ток, протекающий через
сопротивление ![]() ,
а ток, протекающий по емкости
,
а ток, протекающий по емкости 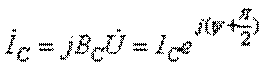 . Ток, потребляемый из источника, будет
равен:
. Ток, потребляемый из источника, будет
равен: 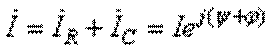 (см.
рис. 4 б).
(см.
рис. 4 б).

Рис. 4.
Практические задания
Задание 1
Изучение переходных процессов заряда и разряда конденсатора
1. Приступая к выполнению данной лабораторной работы необходимо запустить программу ELECTRONICS WORKBENCH.
2. Для работы необходимо собрать следующую схему.
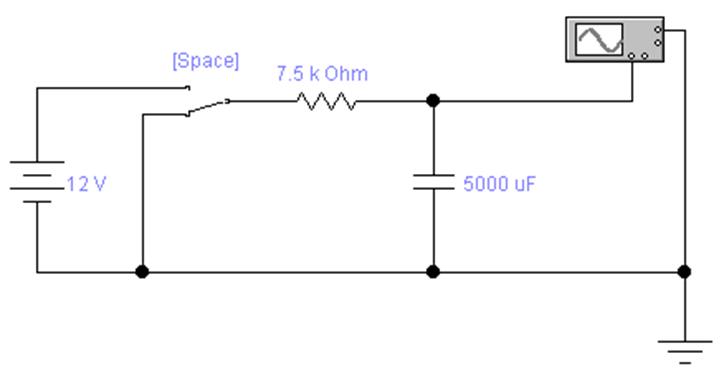
3. Чтобы схема начала функционировать, необходимо
нажать кнопку в верхнем правом углу. ![]()
4. Включить источник ЭДС, ключ замкнуть на источник и наблюдать процесс на осциллографе. При этом на осциллографе в графе TIME BASE выставить цену деления 1с/дел, а на канале А цену деления 5В/дел. Дождаться пока напряжение на обкладках конденсатора станет больше 11,5 В. Переключить ключ и дождаться пока конденсатор разрядится до значения меньше 0,5В. Выбрать пункт меню ANALYSIS→DISPLAY GRAPH. Привести полученный график в удобный для анализа вид.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.