![]()
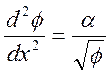 (6.7)
(6.7)
Где
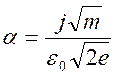 . После умножения обеих частей уравнеия(6.7)
на
. После умножения обеих частей уравнеия(6.7)
на ![]() получаем
получаем
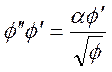 (6.8)
(6.8)
Где штрихами обозначено дифференцирогвание по X . Учитывая, что
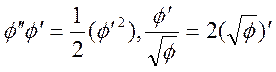
Запишем уравнение (6.8) в виде
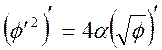 (6.9)
(6.9)
При интегрировании уравнения (6.9) будем использовать граничные условия
![]() (6.10)
(6.10)
Электростатический
потанциал определён с точностью до произвольной постоянной, и ему можно
приписать некоторое значение в люббой точке пространства. Поэтому первое
условие из (6.9) является фактически нормировкой потанциала. Что касается
второго граничного условия, то оно означает равенство нулю напряжённости
электрического поля ![]() на
поверхности катода. Справедливрсть этого условия можно обсновать исходя из
физических соображений. В противном случае при наличии электрического поля
вблизи поверхности катода, все излучаемые термоэлектроны увлеклись бы этим
полем к аноду и электрический ток достигал бы насыщения при любых напряжениях
на лампе. Последовательно интегрируя уравнение (6.9) с учотом граничных условий
(6.10) получаем
на
поверхности катода. Справедливрсть этого условия можно обсновать исходя из
физических соображений. В противном случае при наличии электрического поля
вблизи поверхности катода, все излучаемые термоэлектроны увлеклись бы этим
полем к аноду и электрический ток достигал бы насыщения при любых напряжениях
на лампе. Последовательно интегрируя уравнение (6.9) с учотом граничных условий
(6.10) получаем
![]() (6.11)
(6.11)
Где
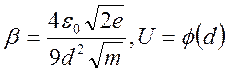 - анодное напряжение, - растояние между
электродами. Такая зависимость между обьемной плотностью анодного тока и
анодным напряжением называется законом Богуславского – Ленгмюра, или законом
трёх вторых.
- анодное напряжение, - растояние между
электродами. Такая зависимость между обьемной плотностью анодного тока и
анодным напряжением называется законом Богуславского – Ленгмюра, или законом
трёх вторых.
Сила анодного тока может быть найдена путём умножения плотности тока (6.11) на площадь анода S. Если электроды имеют форму коаксиальных цилиндров, то зависимость между током и напряжением также подчиняется законну трёх вторых.
![]() (6.12)
(6.12)
Где
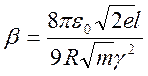 , R и
, R и ![]() – радиус и высота цилиндрического анода,
– радиус и высота цилиндрического анода, ![]() - функция отношения радиусов анода и катода R/r
(при R/r , например при R/r=10 =0.98) В случае
большего отношения R/r формулу(6.12) получить из (6.11) в результате
умножения на площадь анода S=2пRl и использования приближенных соотношений d=R,
- функция отношения радиусов анода и катода R/r
(при R/r , например при R/r=10 =0.98) В случае
большего отношения R/r формулу(6.12) получить из (6.11) в результате
умножения на площадь анода S=2пRl и использования приближенных соотношений d=R, ![]() =1.
=1.
В соответствии с законом Богуславского – Ленгмюра график зависимости 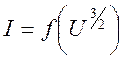 , построеный на основании экспирементальных данных,
должен иметь вид прямой вид прямой линии(рис. 6.4) . Измеряя тангенс угла
наклона прямой относительно оси абсцис, можно определить удельный заряд электрона.
, построеный на основании экспирементальных данных,
должен иметь вид прямой вид прямой линии(рис. 6.4) . Измеряя тангенс угла
наклона прямой относительно оси абсцис, можно определить удельный заряд электрона.
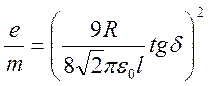 (6.13)
(6.13)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.