Изучение тензора моментов инерции твердого тела

Минестерстово Образования Республики Беларусь

Учреждение Образования  «ГГУ им. Ф.Скорины»

ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ

ТЕМА:

ИЗУЧЕНИЕ ТЕНЗОРА МОМЕНТОВ ИНЕРЦИИ ТВЕРДОГО ТЕЛА

                                                                                                           ВЫПОЛНИЛ:

                                                                                                           СТУДЕНТ ГРУППЫ Ф-11

                                                                                                           Родин Антон Сергеевич

                                                                                                           ПРОВЕРИЛ:

                                                                                                           Тихова Елена Леонидовна

Гомель2005

ЦЕЛЬ РАБОТЫ: осуществить экспериментальную проверку формулы, связывающей момент инерции тела с его главными центральными моментами инерции и построить эллипсоиды тензора моментов инерции данных тел.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: установка FPM-05, набор тел, штангенциркуль.

ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ.

          Момент инерции  некоторого тела относительно оси ON, проходящей через его центр масс, связан с главными центральными моментами инерции  этого тела формулой

     (1)

где ,  и  -направляющие косинусы оси On, т.е. косинусы углов между осью ON и главными осями OX, OY и OZ тензора моментов инерции тела (рис.1).

          Преобразуем соотношение (1) к виду удобному для экспериментальной проверки. Используя известную формулу для периода крутильных колебаний тела вокруг некоторой оси

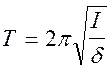
где I -момент инерции тела относительно этой оси,  -момент кручения подвеса, нетрудно получить следующие соотношения

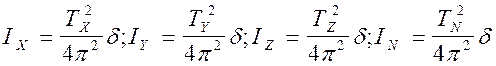     (2)

Здесь , ,  и -периоды крутильных колебаний тела относительно его главных центральных осей и оси ON.

          Согласно рис.2, для направляющих косинусов оси ON исследуемого (параллелепипеда) можем записать

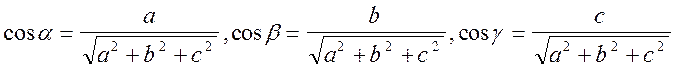     (3)

Подставив (2) и (3) в формулу (1) приходим к соотношению

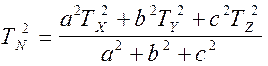     (4)

          Таким образом, задача проверки формулы (1) сводится к проверке выражения (4), устанавливающего связь между линейными размерами тела и периода его крутильных колебаний относительно четырех осей, три из которых являются главными центральными осями.

          Практически для увеличения точности измеряются не периоды крутильных колебаний , ,  и , а продолжительность , ,  и  нескольких полных колебаний. Искомые значения периодов могут быть найдены из простого соотношения

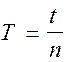     (5)

где t -время, за которое совершается n полных колебаний.

          Соотношение (1) допускает наглядную геометрическую интерпретацию. Изменяя ориентацию оси ON и откладывая вдоль нее значение соответствующего момента инерции , получим геометрическое место точек, образующих эллипсоид, получивший название эллипсоида тензора моментов инерции. Для изучения последнего удобно рассмотреть его сечения координатными плоскостями XOY, XOZ, и YOZ системы координат образованной главными осями OX, OY, OZ.

          Полагая в выражении (1) угол  и учитывая возникающую при этом связь между углами  и 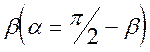, находим уравнение кривой

     (6)

полученной сечением эллипсоида тензора моментов инерции плоскостью XOY. С учетом (2) уравнение (6) принимает вид

     (7)

Аналогично получаются уравнения сечений изучаемого эллипсоида плоскостями YOZ:                                           (8)

ZOX:                                    (9)

          Измерив значение периодов крутильных колебаний , ,  данного тела относительно его главных центральных осей и изменяя значения направляющих углов ,  и  от  до , с помощью соотношений (7-9) можно построить сечения эллипсоида тензора моментов инерции исследуемого тела и сделать выводы о его характере и особенностях.

Описание установки.