Изучение характера вращательного движения при наличии аэродинамических сил сопротивления

ДВИЖЕНИЕ ТЕЛ ПРИ НАЛИЧИИ АЭРОДИНАМИЧЕСКИХ СИЛ СОПРОТИВЛЕНИЯ.

ЦЕЛЬ РАБОТЫ: изучить характер вращательного движения при наличии аэродинамических сил сопротивления, построить графики зависимости пройденного пути от времени, определить коэффициент момента лобового сопротивления пластины, определить момент инерции системы.

ПРИНАДЛЕЖНОСТИ: установка, грузы, секундомер.

КРАТКАЯ ТЕОРИЯ.

          При движении тела в жидкости или в газе оно испытывает сопротивление, которое в частности зависит от относительной скорости тела и частиц среды.

          Сила, с которой среда действует на тело, в общем случае направлена под некоторым углом к направлению движения. Составляющую этой силы, имеющей направление средней скорости потока, называют лобовым сопротивлением. Составляющую, перпендикулярную к скорости потока, называют подъемной силой.

          Лобовое сопротивление складывается из сопротивления вязкости и сопротивления давления. При числе Рейнольдса  меньше критического преобладает сопротивление вязкости

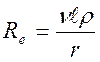     (1)

где    -коэффициент внутреннего трения среды;

 -относительная скорость тела;

 -плотность среды;

 -характерный линейный размер тела (в случае шара - его диаметр).

          При движении тела относительно среды вблизи поверхности его (рис.1) возникает градиент скорости частиц среды и в соответствии с законом Ньютона появляются силы внутреннего трения

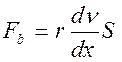     (2)

где    -коэффициент вязкости;

 -площадь соприкасающихся слоев среды;

 -градиент скорости частиц среды.

          При малых скоростях относительно движения для тела, ось симметрии которого совпадает с направлением скорости, распределения скоростей и давлений на тело симметрично. Результирующая давления равна нулю и сопротивление движению оказывают силы внутреннего трения (вязкости).

          Картина обтекания тела резко меняется при возрастании скорости относительно движения. В пограничном слое возрастает градиент скоростей частиц среды, увеличивается торможение частиц вблизи поверхности тела, что ведет к срыву поверхностного слоя и к вихреобразованию. Вследствие вихреобразования в области расположенной сзади тела (рис.2), давление понижено по сравнению с давлением в остальных частях среды. Перед телом возникает область повышенного давления. Число Рейнольдса, в таких условиях, больше критического для данной формы тела и данной среды.

ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКА ИЗМЕРЕНИЯ.

          Установка (рис.3) для изучения характера движения тел, при наличии аэродинамических сил сопротивления, представляет собой стержень 1, который может вращаться вокруг горизонтальной оси 2. На стержне укреплена пластина 3 и груз 4. Последний служит для того, чтобы уравновесить вращающуюся систему тел.

          На цилиндр 5 наматывается нить 6, имеющая на конце груз. Спускаясь, груз приводит во вращение стержень с пластиной. Вся система укреплена на штативе 8, который снабжен шкалой 9 для измерения расстояния, проходимого грузом. Имеется цилиндр 10 большего радиуса. Пластина 3 может быть повернута на любой угол к вектору ее линейной скорости движения, что ведет к изменению лобового сопротивления от значения почти равного нулю, когда скорость пластины совпадает с направлением вектора линейной скорости до некоторого максимального, когда плоскость пластины перпендикулярна к вектору ее линейной скорости.

          Если на цилиндр намотать нить и к концу ее прикрепить груз, то спускаясь он приведет систему во вращательное движение. Запишем уравнение движения груза и вращающейся части установки, используя законы динамики Ньютона

     (3)

и основное уравнение динамики вращательного движения

     (4)

где   -результирующий момент сил, действующую на вращательную систему;

-момент инерции системы относительно оси вращения;

-угловое ускорение вращательного движения.

Будем иметь

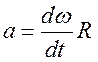     (5)

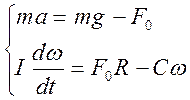     (6)

где   -угловая сила натяжения нити;

-угловое ускорение вращения (-угловая скорость);

-радиус цилиндра, на который намотана нить;

-коэффициент момента лобового сопротивления пластины.

В случае нерастяжимой нити, ускорение груза и угловое ускорение системы связаны соотношением

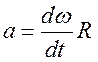     (7)

Из системы уравнений (5) - (7) находим

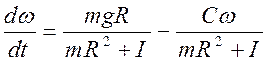     (8)

Введем обозначения

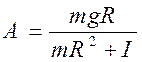     (9)

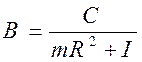     (10)

Тогда

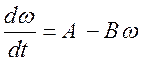     (11)

1. Если  очень мало (практически равно нулю), то

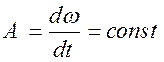     (12)

С учетом (7) и формулы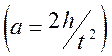

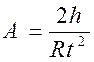     (13)

2. Если , то угловое ускорение максимальное и начальный момент времени уменьшается до нуля, так как с увеличением угловой скорости движения, уменьшается до нуля суммарный момент сил, действующий на систему. Таким образом, наступает момент, когда система вращается с постоянной угловой скоростью. Величина этой скорости находится из формулы (11).

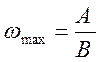     (14)

Максимальная скорость опускания груза

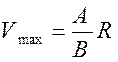     (15)

Значение  можно найти из графика зависимости  при  (рис.4)

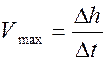
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Установить поверхность пластины так, чтобы лобовое сопротивление было максимальным. Перемещая груз 4, уравновесить вращающуюся систему.

2. Тщательно, виток к витку, намотать нить на цилиндр малого радиуса. К концу нити подвесить груз 7. Нижняя часть груза 7 должна быть на одном уровне с нулевой отметкой шкалы 9.

3. Отпустить груз и пользуясь секундомером, измерить время t опускания груза на расстояние h. Измерение повторить 5-7 раз.

4. Пункт 3 проделать при разных значениях h. Рекомендуется для h взять следующий ряд значений, в см: 5, 10, 15, 20, 25, 30, 40, 50, 70, 90, 110, 130. Данные измерений занести в табл.1 (составить самостоятельно).

5. Построить график зависимости . По графику найти  (рис.4).

6. Установить пластину так, чтобы ее сопротивление было минимальным . Исследовать зависимость  при , как указано в пунктах (2) - (5). Данные измерений занести в табл.2 (составить самостоятельно).

7. Вычислить амплитуду A по формуле (13).

8. По формуле (15) найти B.

9. Величину момента I определить из формулы (9).

10. Коэффициент лобового сопротивления C определить из формулы (10). Все результаты измерений занести в табл.3 (составить самостоятельно).

11. Выполнить пункты (2) - (11), намотав нить на большой цилиндр.

12. Оценить ошибки определения I и C.

ВОПРОСЫ ДЛЯ САМОПОДГАТОВКИ.

1. Стационарное течение жидкости. Основной закон динамики для частицы идеальной жидкости. Уравнение Бернулли. Формула Торичелли.

2. Течение вязкой жидкости. Формула Пуазейля.

3. Лобовое сопротивление тел в потоке. Понятие о законах гидродинамического подобия. Числа Рейнольдса, Фруда, Маха, Струхаля. Их физический смысл.

4. Обтекание крыла вязкой средой. Подъемная сила крыла самолета.

5. Возмущение среды при движении тела со сверхзвуковой скоростью.

ЛИТЕРАТУРА.

1. Сивухин Д.В., Общий курс физики, т.1, Наука, М., 1974, 93-98.

2. Стрелков С.П., Механика, Наука, М., 101, 102, 111, 112, 116, 120, 122.

3. Петровский И.И., Механика, БГУ, Минск, 1973, гл.10.