Вариативные задания на контрольные работы по темам: "Тройной интеграл", "Поверхностные интегралы. Элементы теории поля", "Несобственные интегралы", "Ряды Фурье. Интеграл Фурье", "Комплексные числа", "Ряды. Вычеты. Вычисление интегралов" и "Операционное исчисление". Часть 1

                                            Контрольная работа по теме

                                                “Тройной интеграл”.

                                                          I вариант

1  Расставить пределы интегрирования в интеграле

         
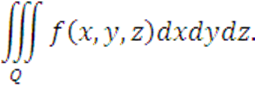
 Изобразить область интегрирования Q,  ограниченную поверхностями: 

,      ,   ,      ,      .

2   Вычислить   

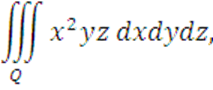
 где область Q ограниченна поверхностями:   ,       ,        .

3  Найти массу пирамиды, ограниченной плоскостями:       ,    , , ,   если   .

4  Вычислить

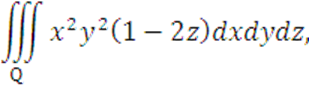
 где Q  - тело, ограниченное поверхностями:    ,  

                                                             II вариант

1  Расставить пределы интегрирования в интеграле

        

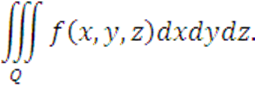
         Изобразить область интегрирования Q,  ограниченную поверхностями: 

          ,      ,   ,      ,      .

2  Вычислить

        

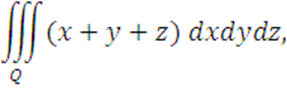
           где область Q ограниченна поверхностями:        ,       ,        .

3   Вычислить  

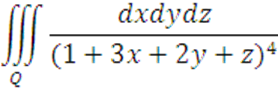
,   где область Q ограниченна поверхностями:        ,     ,        ,      .

4  Найти  объём тела    Q ограниченного  поверхностями:                              ,   

                                                   III вариант

1  Расставить пределы интегрирования в интеграле

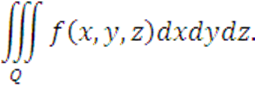
Изобразить область интегрирования Q,  ограниченную поверхностями: 

         ,      ,   ,      ,      . 

2  Вычислить    

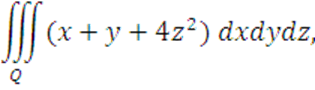
 где область Q ограниченна поверхностями:   ,  ,        .

3  Вычислить  

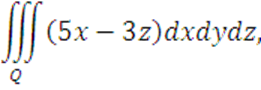
 где область Q ограниченна поверхностями:      ,  ,       .

4  Найти  объём тела    Q ограниченного поверхностями:                              , .

                                                           IV вариант

1  Расставить пределы интегрирования в интеграле

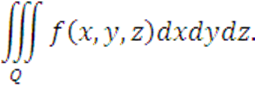
Изобразить область интегрирования Q,  ограниченную поверхностями: 

       ,, ,, .

2  Вычислить   

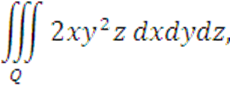
 где область Q ограниченна поверхностями:        ,  ,  .

3  Вычислить  

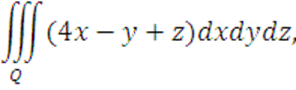
 где область Q ограниченна поверхностями:    ,    ,       ,  .

4  Найти массу тела Q, ограниченной плоскостью:       ,     если   .

                                            V вариант

1  Расставить пределы интегрирования в интеграле

         
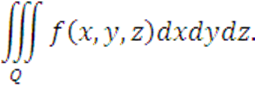
 Изобразить область интегрирования Q,  ограниченную поверхностями: 

,  ,  ,, .

2  Вычислить

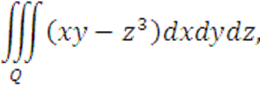
        где область Q ограничена поверхностями:

3  Найти объём тела Q ограниченного поверхностями:    .

4  Вычислить

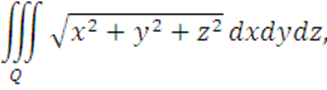
 где область Q ограничена поверхностью:      

                                    VI вариант

1   Расставить пределы интегрирования в интеграле 

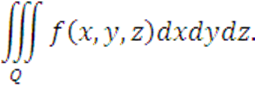
Изобразить область интегрирования Q,  ограниченную поверхностями         ,  , , , .

2  Вычислить 

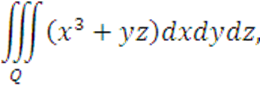
где область Q ограничена поверхностями: 

          

3  Найти массу тела Q, ограниченной плоскостям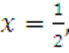и:    ,    , , ,    если   .

4  Вычислить

         

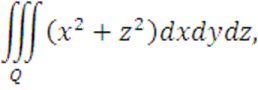
где область Q ограничена поверхностями: 

                                            Контрольная работа по теме

“Поверхностные интегралы. Элементы теории поля”.

                                                          I вариант

1  Формула Остроградского – Гаусса.

2  Вычислить

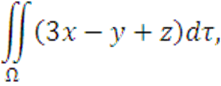
где поверхность   задана уравнением:  и отсечена координатными плоскостями.

3  Вычислить 

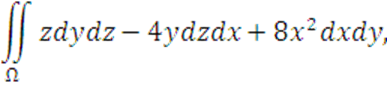
           где поверхность  задана уравнением: и отсекаемая   плоскостью .

4  Вычислить  поток  векторного поля

 через верхнюю часть плоскости , лежащую в первом октанте.

5  Найти ротор векторного поля

.

6  Выяснить, является ли векторное поле  соленоидальным.

                                                          II вариант

1  Определение потенциального векторного поля.

2  Вычислить

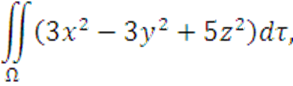
       где  поверхность  задана уравнением:

3  Вычислить

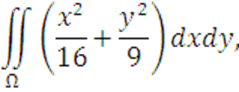
где поверхность  задана уравнением: 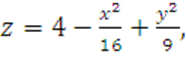 (нормаль внешняя).

4   Вычислить циркуляцию поля   по контуру треугольника, полученного при пересечении плоскости             с координатными плоскостями (обход положительный).

5  Найти дивергенцию векторного поля .

6  Найти grad и (M), если , M(3;1;4)

                                                 III вариант

1  Определение производной по направлению скалярного поля.

2  Вычислить площадь поверхности , расположенную между плоскостями  и .

3  Вычислить  

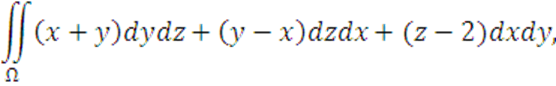
где поверхность  задана уравнением:

4  Вычислить поток векторного поля     ,  по внешней  стороне поверхности  отсекаемой плоскостью .

5  Найти ротор векторного поля     

6  Выяснить, является ли векторное поле  

             соленоидальным.

                                                   IV вариант

1  Написать формулу Стокса.

2  Вычислить

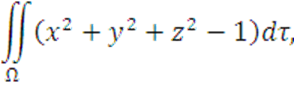
         где поверхность  Ω задана уравнением :

3  Вычислить

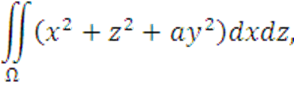
         где поверхность  Ω задана уравнением:  .

4  Найти поток векторного поля       через сторону треугольника, вырезанного из плоскости координатными плоскостями.

5  Найти дивергенцию векторного поля

6  Выяснить, является ли векторное поле , потенциальным.

                                       V вариант

1  Определение градиента функции в точке.

2  Вычислить

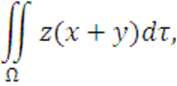
где  поверхность Ω задана уравнением: