Вариативные задания на контрольные работы по темам: "Тройной интеграл", "Поверхностные интегралы. Элементы теории поля", "Несобственные интегралы", "Ряды Фурье. Интеграл Фурье", "Комплексные числа", "Ряды. Вычеты. Вычисление интегралов" и "Операционное исчисление". Часть 1, страница 2

3  Вычислить

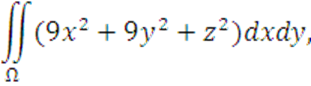
        где Ω  − внешняя сторона поверхности   вырезанная конусом   

4  Вычислить циркуляцию векторного поля    вдоль линии Г пересечения цилиндра  c плоскостью  если .

5  Найти  , если

6  Выяснить, является ли векторное поле  соленоидальным.

                                                      VI вариант

1  Определение соленоидального  векторного поля.

2   Вычислить

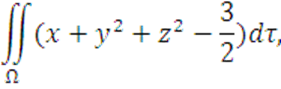
          где  поверхность Ω задана уравнением:

3  Вычислить    

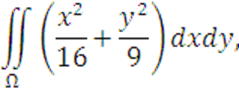
         где Ω  − внешняя сторона поверхности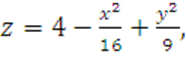 

4  Вычислить линейный интеграл для поля   где L – отрезок АВ: А(2;1;-3), В(1;2;-1).

5  Выяснить, является ли векторное поле потенциальным.

6   Найти производную функции в точке М, по направлению вектора
 ,   M₁(1;0;3), М₂(2;-4;5).

Контрольная работа по теме

“Несобственные интегралы. Интегралы, зависящие от параметра”.

I вариант

1   Вычислить

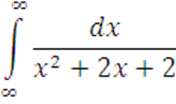
2  Найти производную функции

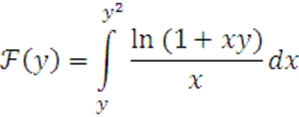
3  Исследовать на равномерную сходимость              

 

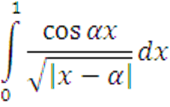
4  Вычислить        

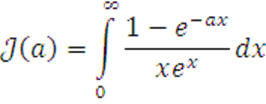
5  Вычислить

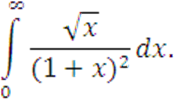
II вариант

1  Вычислить

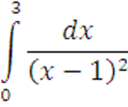
2  Найти производную функции

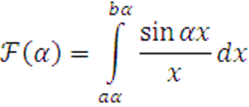
3  Исследовать на равномерную сходимость              

 

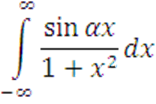
4  Вычислить        

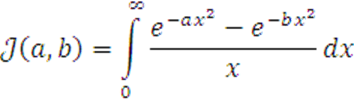
5  Вычислить

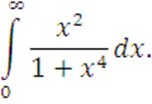
III вариант

1  Вычислить

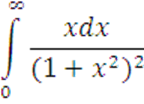
2  Найти производную функции

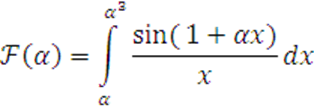
3  Исследовать на равномерную сходимость              

 

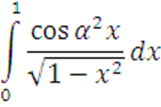
4  Вычислить        

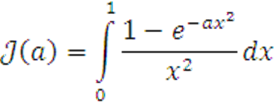
5  Вычислить

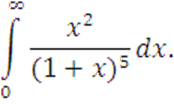
IV вариант

1  Вычислить

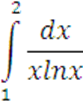
2  Найти производную функции

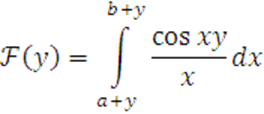
3  Исследовать на равномерную сходимость              

 

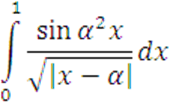
4  Вычислить        

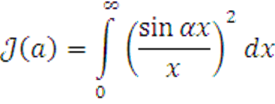
5  Вычислить

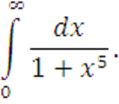
V вариант

1  Вычислить

2  Найти производную функции

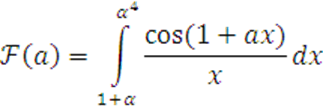
3  Исследовать на равномерную сходимость              

 

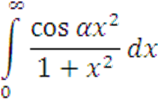
4  Вычислить         

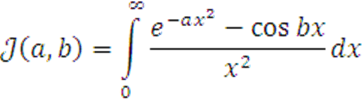
5  Вычислить

VI вариант

1  Вычислить

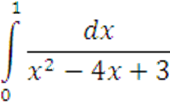
2  Найти производную функции

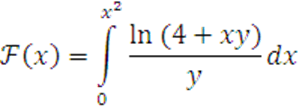
3  Исследовать на равномерную сходимость              

 

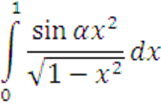
4  Вычислить        

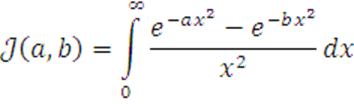
5  Вычислить

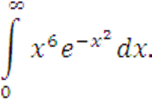
Контрольная работа по теме

“Ряды Фурье. Интеграл Фурье”.

                                                        I вариант

1  Разложить в тригонометрические ряды Фурье функции:

а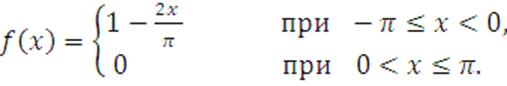   

б 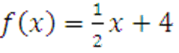  на интервале  по синусам.

в 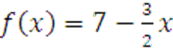   на интервале  по косинусам.

г       на интервале .

д       на интервале  .

е      на интервале .

2     Представить функцию интегралом Фурье

 

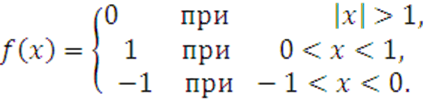
                                                        II вариант

1  Разложить в тригонометрические ряды Фурье функции:

а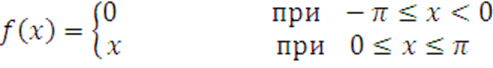   

б   на интервале  по синусам.

в 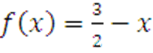   на интервале  по косинусам.

г       на интервале .

д       на интервале  .

е      на интервале .

2   Представить функцию интегралом Фурье

 

                                                       III вариант

1  Разложить в тригонометрические ряды Фурье функции:

а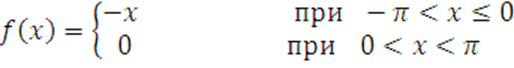   

б   на интервале  по синусам.

в 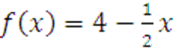   на интервале  по косинусам.

г       на интервале .

д       на интервале  .

е      на интервале .

2   Представить функцию интегралом Фурье

 

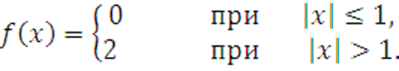
                                                       IV вариант

1  Разложить в тригонометрические ряды Фурье функции:

а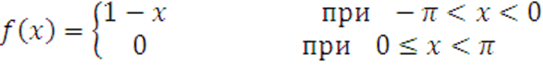   

б   на интервале  по синусам.

в    на интервале  по косинусам.

г 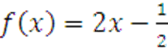      на интервале .

д 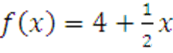      на интервале  .

е      на интервале .