Модель Вальраса. Модели краткосрочного прогнозирования и регулирования экономики

Модель Вальраса

          Модель описывает современную экономическую ситуацию, когда на рынке одновременно действует множество производителей благ и их потребителей. При этом каждый из участников рынка преследует свои цели, поэтому возможны конфликтные ситуации, которые разрешаются через конкурентные рыночные механизмы, основанные на введении регулирующих систем ценообразования.

          При моделировании система ценообразования считается заданной заранее и все сделки подчиняются данной системе. Если участники сделки не могут непосредственно влиять на цены, то рынок называется конкурентным, на конкурентном рынке цены для каждого участника неуправляемы, ему остается только приспосабливаться к их изменению.

          Основной идеей модели Вальраса является то, что при известной системе ценообразования намерения участников сделки являются совместимыми (т.е. все участники тяготеют к разрешению конфликта и заключению сделки). В результате взаимных договоренностей возникает ситуация конкурентного равновесия.

          Предполагается, что в сделке участвуют l потребителей и m производителей, предоставляющих n товаров (под товарами понимают различные блага: продукты труда, средства труда, ресурсы, услуги и т.д.). Тогда строка  р=(р₁ , р₂ , …р_n) – строка цен, а вектор

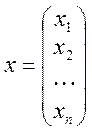 - вектор-столбец товаров.

Пусть каждый потребитель обладает своим доходом K_i(р) и своей функцией предпочтения u_i(x), при этом ему потенциально доступно множество товаров  Х_i(р):

. Тогда функция потребительского спроса задается следующим образом:

.

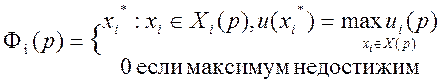Таким образом, каждый потребитель характеризуется своей функцией спроса и доходом. При этом доход каждого потребителя складывается из дохода от продажи первоначального запаса товара p*b_i и из дохода от участия потребителя в процессе производства l_i(p). Т.е. .

Каждый производитель (фирма) характеризуется своими технологическими возможностями. Пусть

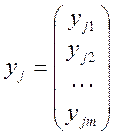 - вектор-столбец затрат-выпусков j производителя.

Положительные компоненты вектора задают выпуски, отрицательные – затраты, тогда скалярное произведение векторов  - прибыльj производителя.

Технологические возможности фирмы определяют множество потенциально допустимых векторов затрат-выпусков Y_k. Это множество называется множеством  производственных возможностей.

          Под функцией предложения производителя понимают один или несколько векторов затрат-выпуска, которые при заданном уровне цен  р позволяют максимизировать прибыль:

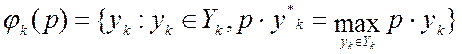
Предполагается, что пространство допустимых выпусков Y_k замкнуто, конечно, а также, что фирма теоретически может не производить никакой продукции и не делать затрат(0 входит в Y_k).

Тогда вектор затрат-выпусков для всей экономики определяется как сумма векторов  затрат-выпусков для всех производителей.

.

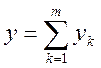При таком суммировании промежуточные продукты взаимно сокращаются, так как в состав векторов затрат-выпусков одних фирм они входят со знаком «+» (как выпуски), а в другие – со знаком « - » (как затраты). В обобщенном векторе затрат-выпусков останутся только первичные ресурсы (отрицательные) и конечные продукты (положительные).

Вектор yпринимает значения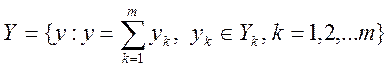

Основной задачей моделирования является математическое описание функций распределения совокупного производства между производителями и распределение произведенных продуктов между потребителями. Функция распределения производства описывает способы выбора векторов затрат-выпусков для каждого из производителей и суммирование их для получения вектора y, описывающего совокупный производственный процесс. Совокупные процессы описывают совокупное  технологическое множество Y(множество производственных возможностей). Сумма первоначальных благ (собственности, которой изначально владеют потребители, выраженной в натуральном или денежном эквиваленте, в виде, например, накоплений) 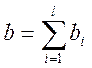представляет собой первоначальную совокупную собственность. В это понятие могут входить как сырьевые ресурсы, так и труд, продукты производства (конечные и промежуточные), средства производства, предметы труда, капиталовложения и т.д.

Вместе множества совокупного производства и первоначальной совокупной собственности формируют вектор совокупного предложения.